Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

ENGF0004

Model 1: Vibrations in a Circular Membrane [100%]

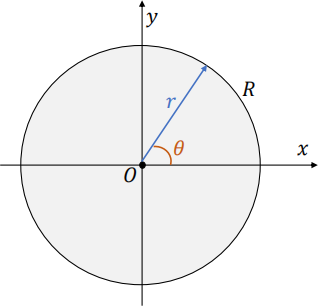
Figure 2. Diagram of a circular membrane with centre at the origin and radius R.

Problem Description

Circular membranes are an important fundamental engineering model - they are essential parts of mechanical pumps, microphones, telephones, and even micro-electromechanical systems (used in numerous sensors). They are so common that they are of relevance to most engineering disciplines. For example, circular membranes are also an essential part of the ear and studied in models of the hearing system in biomedical engineering. Membranes are also important for water treatment to clear out oil from contaminated water, relevant in chemical and environmental engineering. Future satellites are looking to use circular membrane mirrors to improve imaging and communication capabilities.

Understanding how these circular membranes vibrate, either to prevent mechanical failure, or control the vibration to ensure stability or improve efficiency and longevity of the membranes, is of interest in all of these applications.

Having been introduced to the wave equation - a partial differential equation which relates the deflection of the membrane (u(x, t)) as a function of time (t) and space (x, y), you are now capable of modelling these vibrations, which you will demonstrate in this coursework.

The one-dimensional wave equation is given by

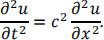
As such, it can be used to only model a one-dimensional problem, such as the vibrations of a string, for example. Modelling the two-dimensional membrane, whereby finding a solution as a function of three variables: x, y and t, is more difficult.

However, we will use an ingenious simplification - we are only interested in solutions which are symmetrical around the centre. This means that the deflection along the radius repeats at any radial line around the circle of the membrane, starting from the centre and ending at the edge. It we sweep the solution we obtain for the deflection along the radius in a 360。arc, we are able to reconstruct what happens on the entire circular membrane. Hence, we will model the vibration along the radius only (one dimension) and have a two-variable solution u(r, t).

We say that such a model is given in polar coordinates: r specifies the position along the radius, and θ specifies the angle around the circle (we assume the solution is the same for all θ).

The model is built on the following assumptions:

1.   The membrane is homogeneous - it has a constant mass per unit area (p = const. ), it is perfectly flexible and does not resist bending.

2.   The membrane is stretched and then fixed along its entire boundary in the rθ-plane. This means the tension per unit length, T, caused by stretching the membrane is constant  and  homogenous  (does  not  change  during  motion  and  is  the  same everywhere).

3.   The deflection, u (r, θ, t), of the membrane during the motion is small in comparison to the size of the membrane and all angles of inclination are small. (This is important for the derivation of the wave equation as the governing equation in the model. By using the wave equation, we assume this is met and use this information no further.)

4.  We will only consider solutions which are radially symmetric. To reiterate, we will model the vibration along the radius only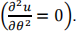

Hence, the deflection, u (r, t), of the circular membrane with a radius R can then be modelled by the wave equation in polar coordinates given by

where

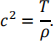
The boundary and initial conditions are given by

u(R, t) = 0 for all time t ≥ 0 (the membrane is fixed along the boundary circle to the support),

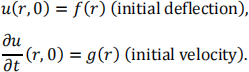
We summarise the model parameters in Table 1.

Table 1. Model variables and parameters.

STAGE 1: Analytical Model [65 marks]

The following questions will help you set up and solve the analytical model, hence they will be more prescriptive in direction.

Question 1 [10 marks]

Demonstrate the separation  of variables technique  applied to  equation  (E1)  in  order  to separate the wave equation into two ordinary differential equations (ODEs).

Question 2 [15 marks]

Write the possible solutions to the time-dependent ODE for G(t) for

.    positive,

.    zero,

.    negative

values of the constant, μ = k2. Discuss why only the negative values of the constant can produce physically viable solutions.

Find the general solution for G(t), if it is known there are infinitely many k values that satisfy the solution.

Question 3 [10 marks]

Now that you have established that the two ODEs found in Question 1 can produce physically meaningful solutions only in the case of a negative constant, μ = −k2, turn to the second ODE. The ODE which describes the solution w(T), depending on the space variable T, then has the form

Use the substitution q = √μT = kT and standard differentiation rules to transform E2 to the Bessel equation (E3)

Question 4 [10 marks]

Solve the Bessel equation using Laplace transforms, taking the initial conditions

w(0) = c,

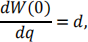
where c and d are constants.

You should make use of the formulae in the standard formula handbook on p.30 and p.32:

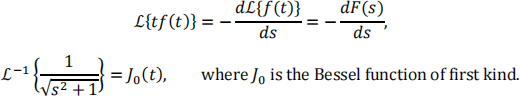
After applying the Laplace transforms, use the standard methods of solving ODEs taught in first year in order to solve the resulting ODE in terms of s.

Question 5 [20 marks]

The solution w(T), depending on the space variable T , found in Question 3 should have the form

w(T) = PJ0 (KT),                                                               (E4)

where P isa constant and K  = √μ is the separation of variables constant.

J0   is the  Bessel function of first  kind and zero order. The Bessel function Jn   is  in-built  in MATLAB through the functionbesselj(nu,Z), where nu = 0 for the zero order function, and z is the function domain, in this case, z  = q.

a)  [5 marks] After reading the information about this function in MATLAB, plot J0 (q)  in MATLAB and find the locations for q at which J0  is 0. This will be useful in finding a solution which matches the boundary condition.

b)  [15 marks] Back in the analytical model, apply the boundary and initial conditions set out in the problem description to find the general form of the solution for the deflection u(T, t) in (E1) .

STAGE 2: Computational Model [35 marks]

The following questions are asking you to set up a computational solution and perform a sensitivity  analysis of the model. They   resemble project-style questions and are less prescriptive.

Question 6 [15 marks]

Having completed the stage 1 questions, you should have found that solutions (or eigenfunctions) representing the membrane deflection  which satisfy the given boundary condition, have the general form

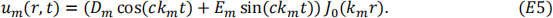
The coefficients Dm  and Em can be evaluate numerically from E6 and E7

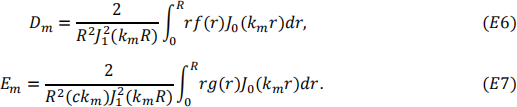
Note that you can choose any functions for the initial conditions f(T) and g(T) - these can be, for example, linear, quadratic, sinusoidal functions.

The solution um describes themth normal mode of vibration. Note that J1 is the Bessel function of first kind and first order.

Use MATLAB to plot solutions for the first three normal modes of membrane vibration given by (E5) form = 1, 2 and 3, at a single time point chosen by you.

Discuss the shapes obtained, paying attention to where the membrane remains stationary (u(T, t) = 0).

Question 7 [20 marks]

Applying the principle of superposition, the complete solution for the deflection of the circular membrane is given by

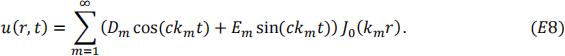
As the last part of your analysis in this coursework, we ask you to consider the effect of model parameters on the amplitude and frequency of the membrane vibrations.

To make it easier to see these effects, use the fast Fourier transform in MATLAB as the main tool in your analysis.

Now explore how different values of the

.    parameter c, and

•    initial conditions, f(r) and g(r),

affect the amplitude and frequency of the membrane vibrations. Discuss and explain your findings.

In your analysis, simulate the effect of three cases each for c, f(r) and g(r), and provide visual proof of at least two of these per parameter as evidence and motivation of your discussion.