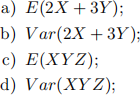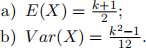Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH 4530 – Probability

Autumn 2021

Homework 7

Problem 1 (p. 182, #6): (3 points)

Let X be the number of spades in 7 cards dealt from a well-shuffled deck of 52 cards containing 13 spades. Find E(X). [Hint: Use the method of indicators.]

Problem 2: (3 points)

Let X be a discrete random variable with RX = {0, 1, 2, 3} and the following distribution:

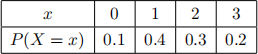
Problem 3 (p. 202, #3): (4 points)

Let X, Y , and Z be independent identically distributed random variables with mean 1 and variance 2. Calculate:

Problem 4 (p. 202, #9): (3 points)

Out of n individuals vote at an election, r vote Republican and n − r vote Democrat. At the next election the probability of a Republican switching to vote Democrat is p1, and of a Democrat switching is p2. Suppose individuals behave independently. Find the expectation and the variance of the number of Republican votes at the second election.

Problem 5: (4 points)

Suppose that X has uniform distribution on the set {1, 2, . . . , k}. Show:

Problem 6 (p. 203, #15): (1+2=3 points)

a) Show that if X and Y are independent random variables, then

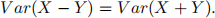
b) Let D1 and D2 represent two draws at random with replacement from a population, with E(D1) = 10 and SD(D1) = 2. Find a number c so that

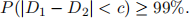
Problem 7 (p. 182, #8):

Suppose E(X² ) = 3, E(Y² ) = 4, E(XY ) = 2. Find E [(X + Y )²].

Problem 8:

Let X and Y be two independent random variables. Suppose we know that V ar(2X − Y ) = 6 and V ar(X + 2Y ) = 9. Find V ar(X) and V ar(Y ).

Problem 9 (p. 202, #4):

Suppose X1 and X2 are independent. Find a formula for V ar(X1X2) in terms of µ1 = E(X1), 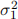 = V ar(X1), µ2 = E(X2), and  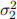= V ar(X2).

Problem 10 (p. 203, #13):

Suppose the IQ scores of a million individuals have a mean of 100 and an SD of 10.

a) Without making any further assumptions about the distribution of the scores, find an upper bound on the number of scores exceeding 130.

b) Find a smaller upper bound on the number of scores exceeding 130 assuming the distribution of scores is symmetric about 100.

c) Estimate the number of scores exceeding 130 assuming that the distribution is approximately normal.