Math 447: Real Variables Homework 11
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Homework 11
Math 447: Real Variables
Exercise 1 For each function below, derive the power series expansion in a neighborhood of 0 and determine the interval of convergence. Justify your answer by showing all your work.
(a) 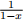
(b) 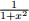
(c) arctan x
Exercise 2 Let O Rn be a connected open subset and let f : O ! R be a function such that each partial derivative ∂f/∂xi exists and is continuous (that is, for each i = 1, . . . n, the single-variable function fi obtained by holding all xj constant except xi is continuously diferentiable 1 ).
(a) (The n-dimensional Mean Value Theorem) Let p0 2 O and let ε > 0 such that B" (p0 ) O. Let p 2 B" (p0 ) and put p - p0 = (Δx1 , Δx2 , . . . , Δxn ). Prove that there are points p1 , . . . pn 2 O such that
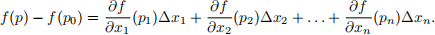
Note: You may use the single-variable mean value theorem.
(b) Prove that f is diferentiable and that in particular
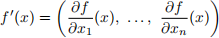
satisies the deinition of the derivative of f given in Lectures 30 and 31. Note that you need to show that
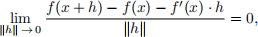
or, equivalently, that for each x 2 O and ε > 0 such that Bε (x) O 9δ such that
y 2 Bδ (x) =) |f (y) — f (x) — f、(x) · (y — x)| < |d(x, y)jε .
Note that in both expressions “ · ” denotes the scalar product of two vectors.
(c) Suppose K is a compact subset of O and ε > 0. Show that 9δ such that for any x 2 K
||h|| < δ => |f (x + h) — f (x) — f'(x) · h| < ||h||ε .
Note that this is a stronger result than part (b) because the limit is uniform (independent of x) on K.
Exercise 3 Let O Rn be an open set and let f : O ! Rm . Denote the component functions by (fi ![]() f = (f1 , . . . fm ). That is, each fi is an n-variable function O ! Rm , and
f = (f1 , . . . fm ). That is, each fi is an n-variable function O ! Rm , and
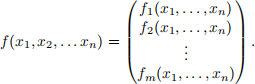
Assume additionally that each partial derivative ∂fi /∂xj exists and is continuous. Prove that f is diferentiable (according to Lectures 30 and 31) and that
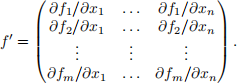
Note that again you must show that
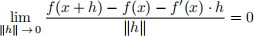
(or equivalent expression similar to that given in part (b)). Here f、(x) denotes the result of evaluating each partial at x, i.e., ∂fi /∂xj (x), and “ · ” denotes the matrix product, where h is regarded as a column vector (n X 1 matrix).
2024-01-02