Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Infinite-horizon path following- Draft version

Assignment 2, 4SC000, TU/e, 2023-2024

where, as usual xk  ∈ Rn  and uk  ∈ Rm , are the state and control input, respectively, and zk  ∈ Rp is an output that should track a given reference. The disturbance sequence {wk |k ∈ {0, 1, . . . , h-1}} is assumed to be a sequence of independent and identically distributed random variables with covariance E[wkwk(「)] = W.  While the assignments below only consider the case W  = 0, i.e., the disturbances can be assumed to be zero wk  = 0 for every k, the problem is formulated for the general case.  Consider also a spatial path γ(s) ∈ Rp  parameterized by s ∈ (-∞ , ∞) and generated by a so-called exosystem

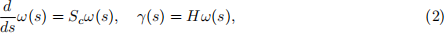
with ω(s) ∈ Rn!    for every s ∈ {-∞ , ∞}.  As usual for exo-systems, it is assumed that  Sc  has all its eigenvalues on the imaginary axis.  The reference is taken along a path.  By considering a given time profile for the parameter s,-the path becomes a trajectory r(t) = γ(s(t)).  Let v(t) be such that ˙(s)(t) = v(t),   s(0) = s,   s(t) = . To account for the chosen discrete-time setting, the considered trajectory speed is assumed to be piecewise constant v(t) = vk , t ∈ [kτ, (k + 1)τ ), leading to

with  s0   = s and  sk   =  s(tk )  so  that  the sampled reference/trajectory takes the form  rk   =

γ(sk ),   k ∈ Z.  For trajectory tracking with constant speed vc , ˙(s) = vc  in which case

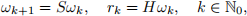
where ωk  = ω(kτ ) and S = eSc τ vc    has all its eigenvalues on the unit circle.  In the path-following case

for decision variables vk .   Let ζk   =  [xk(「) ωk(「)]「 and  IaIR(2)  =  a「Ra  for an arbitrary vector a.

Moreover, consider stationary policies θ = (µ, σ) for the control uk  = µ(ζk ) 2 Rm  and speed

inputs vk  = σ(ζk ) 2 W` , ` 2 f1, 2g.  The path-following problem is then captured by posing the following stochastic optimal control problem: find θ to solve

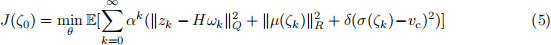
for positive semi-definite Q and R, which are tuning matrices, and for a given weight δ > 0 which is an additional tuning variable.  The discount factor 0 < α 1 needs to be strictly smaller than one either when the disturbances are not zero ( W > 0) or when the input is penalized (e.g. R > 0),since otherwise (5) is generally unbounded. As usual, a penalty on the control input is added for regularization.

Trajectory tracking

It can be shown that the optimal policy when vk  = vc  for every k 2 Z takes the form

Path-following

Solving (5) is in general a hard problem. Still we can design a simple policy using rollout/MPC ideas which can be shown to yield a better cost than the trajectory tracking policy.  To this end, let

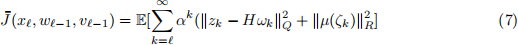
when

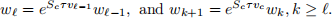
and consider the suboptimal policy

Intuitively, the path following strategy can choose when the trajectory along the path starts, assuming at each iteration it will have constant velocity from that point onwards  (although iteratively this velocity will in general change). The advantage of having this degree of freedom is illustrated in Figure 1.