MATH5816 Continuous Time Financial Modelling
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH5816 Continuous Time Financial Modelling
Assignment 1, 2021
Instructions: This is a group assignment (up to 3 person per group) which is worth 10% of the total assessment. The assignment must be submitted online to turnitin on moodle before 7pm on Wednesday Week 4. There will be two turnitin submission boxes, one for the group and one for each individual. Everyone in the group should submit a copy of the assignment to the individual submission box and only one member of the group should upload their assignment to the group submission box. Only the copy submitted to the group submission box will be marked.
Exercise 1. Suppose for t ∈ [0, T] that X satisfies the SDE
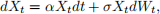
and Y satisfies
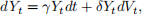
where V is a Wiener process which is independent of W.
1. Define Z by Z = XY and derive the stochastic differential equation satisfied by Z. Note that if X describes the price process of an APPLE in USD and Y is the currency rate AUD/USD then Z describes the dynamics of the APPLE stock expressed in AUD.
Exercise 2. Let X and Y be the solution to the following system of SDEs
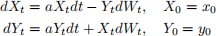
where W is a Brownian motion and x0, y0 are constants.
1. Show that
is a deterministic process.
2. Compute
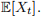
Exercise 3. Let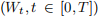 
be a one-dimensional standard Brownian motion defined on a filtered probability space 
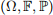endowed with the filtration 
1. Show that the process (St, t ∈ [0, T]) given by the formula, for every
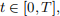
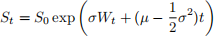
where
is the unique solution of the stochastic differential equation (SDE)
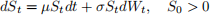
Hint: To establish S is a solution, it is sufficient to apply the
formula and the uniqueness of a solution to SDE (1), assume that
is another solution to equation (1) with
and use the
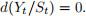
2. Using the
by the processes
and
Recall that
and
is a martingale.
3. Apply the Girsanov theorem in order to find the unique probability measure
on
under which the process
is a martingale. Write down the dynamics of
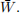
2021-10-12