CSC373 Fall’20 Final Assessment
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CSC373 Fall’20
Final Assessment
Date: December 18, 2020
Instructions
1. You can print this PDF and use the blank space provided after each question to write your solution. You can also prepare a PDF of your solutions digitally or by writing on blank paper.
2. Upload a single PDF with your solutions to MarkUs at https://markus.teach.cs.toronto.edu/csc373-2020-09
3. For handwritten solutions, please make sure that your handwriting is legible and that your scan is high-quality.
4. Remember: You receive 20% for any (sub)problem if you leave it blank (or cross off any written solution) and write “I do not know how to approach this problem.”. You receive 10% if you leave it blank but do not write this or a similar statement.
5. Remember: You may fail the course if you achieve a grade lower than 40% on this final assessment.
Q1 [10 Points] Find the Single Attendee
There are 2n + 1 attendees at a party, which includes n couples and a single person. At the end of the party, all the attendees form a line in which each person stands next to their partner, except for the single person, who stands somewhere in the line. As an example, for n = 3, the seven attendees could be standing in the order (A1, A2, B1, B2, C, D1, D2), where (A1, A2), (B1, B2), and (D1, D2) are couples and C is single.
Your job is to find the position of the single person (this would be 5 in the above example). But you don’t know which ones are partners. All you can do is ask questions of the form “Are the i-th and j-th people in the line partners?” Design a divide-and-conquer algorithm for this problem which finds the position of the single person by asking O(log n) questions. Justify your answer.
Q2 [15 Points] Event Planner
There are n events, each takes one unit of time. Each event i will provide a profit of gi dollars if it is started at or before time ti , but will provide zero profit if it is not started by time ti (so there is no point in scheduling event i unless it can be scheduled to start by time ti). Here, gi , ti ≥ 0 and ti may NOT be an integer. An event can start as early as time 0 and no two events can be running simultaneously. The goal is to feasibly schedule a subset of the events to maximize the total profit.
(a) [2.5 Points] Prove that there exists an optimal schedule OP T in which every event that is scheduled is scheduled to start at an integral time. Note that in such a solution, each event i is either scheduled to start by time b tic or not scheduled at all.
(b) [5 Points] Design an efficient greedy algorithm which only schedules events at integral start times. [Hint: Let T = maxib tic . Think about which event you would schedule to start at time T.]
(c) [5 Points] Prove that your algorithm always returns an optimal solution.
(d) [2.5 Points] Analyze the worst-case running time of your algorithm. Explicitly state the data structures that your algorithm uses.
Q3 [15 Points] Protect the Paintings Again
Recall the question about protecting paintings from midterm 1. A corridor of a museum is rep-resented by the interval [a, b] (with a < b) and contains valuable paintings. There are n guards stationed along the corridor. Guard i can protect the interval [si , fi ], where a ≤ si ≤ fi ≤ b. We say that a subset of guards P ⊆ {1, . . . , n} is acceptable if the guards in P already collectively protect the entire corridor, i.e., ∪i∈P [si , fi ] = [a, b]. Assume that the set of all guards {1, . . . , n} is acceptable, so there is at least one acceptable set.
In the midterm, we designed a greedy algorithm for finding an acceptable subset P of minimum cardinality |P|. Instead, suppose that each guard i has an associated non-negative cost ci . Design a dynamic programming solution for finding an acceptable subset P with the smallest total cost P i∈P ci . For full credit, your solution must run in O(n 2 ) time and space.
[Hint: Consider the set of all the “breakpoints”: {a, b, s1, f1, s2, f2, . . . , sn, fn}. Suppose the distinct breakpoints in the ascending order are a = p1 < p2 < . . . < pm = b for some m. It may be useful to think of a subproblem where you want to cover the sub-interval [p1, pj ] using only some of the guards. Do not forget to bound the maximum number of distinct breakpoints m in terms of n.]
(a) [5 Points] Define an array storing the necessary information from subproblems. Clearly define what each entry means and how you would compute the desired solution given this array.
(b) [5 Points] Write a Bellman equation and briefly justify its correctness.
(c) [2.5 Points] In what order would you compute the entries in a bottom-up implementation?
(d) [2.5 Points] Analyze the worst-case running time and space complexity of your algorithm.
Q4 [15 Points] Divide the Workload
You are the CEO of a company which employs n workers to perform m tasks. Each worker i is supposed to work a total of wi hours and each task j requires a total of tj hours of work. Assume that P ni=1 wi = P mj=1 tj . The floor supervisor has come up with an ideal work schedule represented as matrix A, where row i represents worker i, column j represents task j, and Ai,j is the number of hours worker i will spend on task j. Matrix A has the property that the sum along each row i is exactly wi and the sum along each column j is exactly tj .
There is just one problem. The floor supervisor has taken the liberty of using fractional values for Ai,j -s, forgetting the recent company policy that a worker must spend an integral number of hours on a task. Luckily, all the wi-s and tj -s are integral. Your goal is to prove that it is always possible to “round” matrix A into some matrix B while preserving the row and column sums (i.e. set each Bi,j to be either b Ai,jc or d Ai,je such that each row i of B still sums to wi and each column j of B still sums to tj ). The example below shows such a rounding of a 3 × 3 matrix.
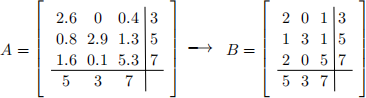
(a) [2.5 Points] Consider the matrix A0 obtained by replacing each entry of A with its fractional part (e.g. replacing 1.3 with 0.3, 2.6 with 0.6, 0.1 with 0.1, etc). First, argue that A0 must also have integral row and column sums. Next, argue that if A0 can be rounded while preserving the row and column sums, then A can be as well.
(b) [10 Points] Note that each A0i,j ∈ [0, 1]; hence, rounding it means setting it to either 0 or 1 (ex-cept, if A0i,j ∈ {0, 1} then the rounding must not change its value). Using network flow techniques, show that A0 can be rounded while preserving row and column sums. Justify your answer.
[Hint: Construct a network with integral edge capacities, use A0 to construct a max flow with fractional flow values on edges, and then use the integrality property of the Ford-Fulkerson algorithm (i.e. that it finds a max flow in which each edge carries an integral amount of flow).]
(c) [2.5 Points] What is the worst-case running time of the na¨ıve Ford-Fulkerson on your network?
Q5 [15 Points] Linear Programming
(a) [5 Points] Convert the following linear program to the standard form. You only need to write the final answer; no justification is needed.

(b) [5 Points] Write the dual of the linear program from part (a). You do not need to write this in the standard form and no justification is needed.
(c) [5 Points] Consider the optimization problem from part (a), but change the objective function to maximizing f(x, y, z), where
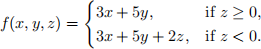
Note that f(x, y, z) is not linear, and hence, the new optimization problem is not linear as well. Nonetheless, show that it can be converted into an equivalent linear program. Provide this equiv-alent linear program in its standard form and justify the equivalence.
Q6 [20 Points] SAT
Recall that a CNF formula ϕ = C1 ∧ . . . ∧ Cm is a conjunction of clauses, where each clause is a disjunction of (any number of) literals. Recall the NP-complete problem SAT.
SAT:
Input: A CNF formula ϕ.
Question: Does ϕ have a satisfying assignment?
Now, consider the following two variants of it.
TripleSAT:
Input: A CNF formula ϕ.
Question: Does ϕ have at least three different satisfying assignments?
TwoThirdsSAT:
Input: A CNF formula ϕ.
Question: Is there an assignment satisfying at least two-thirds (2/3) of the clauses of ϕ?
(a) [3 Points] Prove that TripleSAT is in NP.
(b) [7 Points] Prove that TripleSAT is NP-hard through a reduction from SAT.
(c) [3 Points] Prove that TwoThirdsSAT is in NP.
(d) [7 Points] Prove that TwoThirdsSAT is NP-hard through a reduction from SAT.
Q7 [15 Points] Sabotage!
There is an undirected graph G = (V, E), where nodes in V are servers and edges in E are cables running between pairs of servers. A set of k > 2 servers S = {v1, . . . , vk} ⊆ V is trying to collabo-ratively solve a problem and you want to sabotage this!
Specifically, you want to remove a subset of edges T ⊆ E such that all nodes in S become discon-nected from one another (i.e. there is no path left between any two of them). You want |T| to be as small as possible. Consider the following greedy algorithm.
Algorithm 1: Greedy-Sabotage
1 for i = 1, . . . , k do
2 Let Ei be the smallest subset of edges we need to remove to disconnect vi from every other node in S. (It turns out that Ei can be computed efficiently, but do not worry about this.)
3 end
4 Remove the union of k − 1 smallest Ei-s (i.e. the union of all but the largest Ei).
(a) [5 Points] Prove that Greedy-Sabotage returns a feasible solution T (i.e. removing the set of edges T it returns will indeed disconnect every pair of nodes in S).
(b) [10 Points] Prove that Greedy-Sabotage achieves a 2 − 1/k approximation ratio. For partial credit, prove a slightly weaker approximation ratio of 2.
[Hint: Let T ∗ denote the optimal solution. For each i ∈ {1, . . . , k}, let Vi ⊆ V denote the set of nodes in the connected component containing vi (but no other node in S) that remains after removing T ∗ . Can you relate the number of edges in T ∗ with one endpoint in Vi with |Ei |?]
2023-12-21