Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Math 4281, Practice Problems for Exam 1

Problem 1. What are the definitions of a group, a subgroup, an abelian group, a cyclic groups, and a group homomorphism?

Problem 2. Give a proof of Lagrange’s theorem: the order of the subgroup H is the divisor of the order of the group G.

Problem 3. Give a proof of Cayley’s theorem: every finite group G is isomorphic to a subgroup of the symmetric group Sn where n is the order of G.

Problem 3. Consider the absolute value map φ : C^× → R^× sending a non-zero complex number z = a+bi to (a² +b²)^1/2 . Is φ is group homomorphism where the group structures on C^× and R^× are given by multiplication. If yes, please describe the image and kernel of φ, if not, please explain why.

Problem 4. Let G = GL2(R) be the group of all 2 × 2 invertible matrices.

(a) Is G an abelian group?

(b) What is the center of G?

(c) Show that the determinant map det : G → R^× is a group homomorphism.

(d) Show that the map φ : G → G sending A to (A^t)⁻¹ is an isomorphism.

Problem 5. Let f123 ∈ S3 be the bijection (or permutation) sending 1 to 2, 2 to 3, and 3 to 1. Consider the cyclic subgroup H generated by f123. Write down the right coset of H in S3. What is the index of H in S3.

Problem 6. Let G be a cyclic group of order 6. How many of its elements generate G?

Problem 7. Let φ : G → G' be a surjective morphism, that is, an epimorphism. Show that if G is cyclic, then G' is cyclic. Show that if G is abelian, then G' is abelian.

Problem 8. Let G be a group. Show that the relation a ~ b if a = xbx⁻¹ for some x ∈ G is an equivalence relation on G.

Problem 9. Consider the dihedral group D3 = {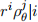 = 0, 1 and j = 0, 1, 2} generated by the rotation ρθ, where θ = 2π/3, and the reflection r about the x-axis.

(a) What are the subgroups of D3?

(b)(Optional) Show that the groups D3 and S3 are isomorphic.

Problem 10. Consider the following operation ” ○ ” on Zn = {[0], [1], ..., [n − 1]} given by [a] ○ [b] = [ab]. Does ” ○ ” define a group structure on Zn?

Problem 11. Consider the group Z6 = {[0], [1], ..., [5]}.

(a) What is the order of the element [4] in Z6

(b) Let H be the cyclic subgroup generated by [4]. What are the cosets of H in Z6?