Macroeconomic Theory (AS.440.602) Fall 2023 Problem Set 4
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Macroeconomic Theory (AS.440.602)
Fall 2023
Problem Set 4
1) The representative agent consumes two goods (x andy) with respective prices Px and Py . The income of the agent is denoted by I and the utility function reads:
U(x, y) = αln(x)+ (1−α)ln(y)
a. Solve the optimization problem of the agent by substituting the budget constraint into the utility function.
b. Write the Lagrangian problem and solve it. In particular, show how the demand for each good is affected by Px , Py and I . Discuss!
c. Show the results for the special case of Px = 2Py and α = 1/2.
2) The representative agent lives for two periods (1 and 2) and receives exogenous incomes of y1 and y2 , respectively. The lifetime utility function is given by:
V(c1 , c2 ) = ln(c1 )+ βln(c2 )
with β(<1)being the discount factor.
The agent is allowed to save or borrow at the real interest rate r , but she cannot die with debt or wealth. Assume also that the initial wealth is zero.
a. Derive the intertemporal budget constraint (IBC) of the agent.
b. Solve the optimization problem of the agent. In particular, show the Euler equation.
c. Find the optimal value of c1 as a function of the parameters and the exogenous variables of the problem.
d. Assume y1 = y2 and β(1+ r) = 1. Is the agent saving or borrowing?
e. Assume y2 = (1+ r)y1 and β(1+ r) = 1. Is the agent saving or borrowing?
f. Assume y1 = (1+ r)y2 and β(1+ r) = 1. Is the agent saving or borrowing?
3) The representative agent lives for two periods (1 and 2) and receives exogenous incomes of y1 and y2 respectively. The lifetime utility function is given by:
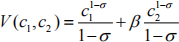
with β(< 1)being the discount factor.
The agent is allowed to save or borrow at the real interest rate r , but she cannot die with debt or wealth. Assume also that the initial wealth is zero.
a. Solve the optimization problem of the agent using the period by period budget constraints. In particular, show the Euler equation.
b. Find the optimal value of c1 as a function of the parameters and the exogenous variables of the problem.
c. Find the optimal value of c2 as a function of the parameters and the exogenous variables of the problem.
d. What is the intertemporal elasticity of substitution (IES)?
4) The representative agent lives for T periods (0, 1, 2, … T- 1) and receives exogenous incomes of y0 ,y1 ,y2 ,...,yT−1 , respectively. The lifetime present discounted value of utility is given by:
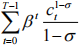
with β(< 1)being the discount factor.
The agent is allowed to save or borrow at the real interest rate r , but she cannot die with debt or wealth. Assume also that the initial wealth is zero.
a. Solve the optimization problem of the agent using the period by period budget constraints. In particular, show the Euler equation.
b. Show optimal ct as a function of c0 (and other the parameters or exogenous variables).
c. Letσ = 1and use your answer for part b to find the present discounted value of lifetime
consumption as a function of c0 (and other parameters or exogenous variables).
d. Re-do part c when T goes to infinity ( ∞ ).
2023-12-20