MATH 108B PRACTICE FINAL
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH 108B
PRACTICE FINAL
Note: You may use without proof any of the results from lectures or homeworks, but in that case you should clearly state what you’re using.
Problem 1. Consider the linear transformation
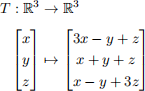
and let A 2 M3x3 (R) be the standard matrix of T.
(a) Determine whether A is diagonalizable, and if so, ind an invertible matrix S such that S-1 AS is diagonal.
(b) Let B = [T]B be the matrix of T associated to an arbitrary basis B of R3 . Is B diagonalizable? Justify your answer.
Problem 2. Let T : V ! V be an invertible linear transformation.
(a) Show that if λ is an eigenvalue of T, then λ 
0, and λ -1 is an eigenvalue of T-1 .
(b) Show that for any eigenvalue λ of T, we have the following equality of eigenspaces:
E (T) = E - 1 (T-1).
Problem 3. Find values of a,b, c 2 R such that
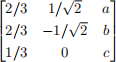
is an orthogonal matrix.
Problem 4. Let A 2 Mnxn (R) be a symmetric matrix, and consider Rn with the dot product. Show that if ~v1 , ~v2 2 Rn are eigenvectors of A with diferent eigenvalues, then ~v1 and ~v2 are orthogonal.
(Hint: Use the formula for the dot product in terms of matrix multiplication.)
Problem 5. Let J be the Jordan canonical form of
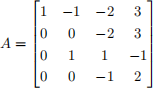
Find J and an invertible matrix S such that S-1 AS = J.
2023-12-16