Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH 240E: HOMEWORK #1

Note: The engineering section of math 240 will not use “make-up” Friday quizzes. Instead we will periodically assign homeworks. The goal of these homeworks is to illustrate additional applications to science and engineering, and to encourage more in-depth thinking than is possible on a quiz. As a result our grading system will be different than that of the other sections, with less weight on quizzes and more weight on homework.

1. An application of column spans to testing

    Please look at the the “Mathwhile” video in the week 6 module of the canvas site of the course. Then work on the following application of the same ideas to medical testing.

The Scenario: Suppose that a group of m ≥ 1 people in a vaccine trial have been given an experimental vaccine. Each person in the group is then given n ≥ 1 tests for various possible side effects. This results in an m × n matrix

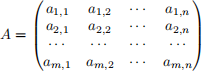
in which ai,j = 1 in Z/2 = {0, 1} if the i^th person had side effect j and ai,j = 0 if they did not have this side effect. Thus rows correspond to test subjects, and columns correspond to tests.

    Eventually the vaccine will be given to the general population. The goal of the trial is to develop an efficient way to predict all the side effects a given person will have. It is expensive to perform all n tests on each person in the general population. So we would like to find a minimal number of tests such that once one knows the results for those tests, one can predict the outcome on every test.

Some definitions: Recall that the column space Col(A) of A is the space spanned over Z/2 by the columns. In other words, Col(A) is the space of column vectors in (Z/2)^m which are linear combinations with coefficients in Z/2 of the columns of A. Similarly, the row space Row(A) is the subspace of (Z/2)ⁿ spanned by the rows.

    The dimension of a vector space is the number of elements in a basis for the space, which is the size of a minimal generating set and the maximal size of an independent subset.

    The rank Rank(A) of a matrix A is the dimension of Row(A). If 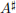is row equivalent to A, then Row(A) = Row(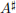). So Rank(A) = Rank(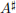) equals the number of non-zero rows of 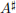, which is the number of pivot entries in .

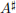Problems:

1. Suppose J is a set of column indices such that the columns of A indexed by j ∈ J form a basis for Col(A). Explain why the test results indexed by J for any member of the vaccine trial are sufficient to determine all the test results of that person.

Hints: The hypothesis implies that for every 1 ≤ k ≤ n, there are constants rj ∈ Z/2 = {0, 1} such that the k^th column of A equals

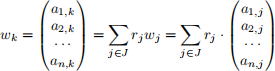
Suppose a member of the vaccine trial group corresponds to row index i. How would you determine the result ai,k of their k^th test from the results {ai,j}j∈J of the tests indexed by J?

2. What conditions on the matrix A are equivalent to not having to do any tests at all to determine which side effects a person would have? What condition on Rank(A) is equivalent to this? What condition on the dimension of Col(A) is equivalent to this?

Note: First think about the difference between these statements:

i. Every individual test gives the same result for every person in the trial group, this result depending on the test.

ii. For each person in the trial group, every test gives the same result, with this result depending on the person.

For each person we want to be able to predict with no test results about them what the outcome of each test will be for them. Which of (i) and (ii) corresponds to being able to do this? Then think about what this means about the matrix A.

Warning: A vector space can have a single element, namely the additive identity element, and in this case the vector space has dimension 0.

3. The Mathwhile video explains why a set of columns of A is linearly independent if and only if the corresponding columns of a reduced row echelon matrix equivalent to A are independent. Use this and problem #3 to determine a minimal set J of tests to use when A is the matrix

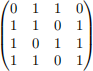
4. Suppose A is the matrix

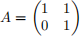
Show that any set of columns which span the column space of A must contain both columns of A. On the other hand, suppose as above that the rows of A represent the test results of two people to two true/false tests. Is it true that all the test results of every person are determined by their first test result?

5. The goal we have been discussing is to find a set J of tests which is sufficient to predict the outcome of a person on any test. Show that saying the columns in J generate the column space of A is equivalent to an extra condition on how this prediction should be made. How would you formulate such a condition on how the result of the k^th test should be predicted in terms of the results of the tests indexed by J?

Hint: Think about the existence for each k of a set of constants indexed by J.

A comment on real world limitations: The method developed here is based all the test results for a vaccine trial group of m people. One could imagine, for example, that m is around 10,000. We want a protocol which can be applied to a much larger general population. For instance, the U.S. population is over 328,000,000. For the method developed in these problems to be rigorously correct for everyone in the (large) general population, we would need to assume that everyone in the (large) general population has exactly the same responses to the tests as at least one person in the (small) trial group.

    The odds are that in fact, the trial group is not strictly representative for everyone in the general population. It is likely that a very small fraction of the general population will not have the same test results as anyone in the trial group, e.g. if there are 10,000 people in the trial and 328,000,000 people in the general population. However, this is likely to lead to errors for only a small percentage of the general population. So using the results of the trial to devise an efficient protocol for the general population would still be a good idea. More people could be quickly tested and saved from dangerous side effects, even if a small percentage of people in the general population are not correctly diagnosed for all side effects.