Due:  Saturday, August 20th, 9am (New York Time)

1    Problem 1

Consider a linear time invariant system ˙(x) = Ax,  x(0) = [0, 1, 1]T  ∈ R3  with

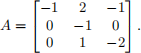
1.  Find the Jordan canonical form of A and give the transformation matrix.

2.  Find the solution of the differential equation under given initial conditions.

3.  Let A be perturbed by a constant a ∈ R and

Find the possible values of a such that the system ˙(x) = Ax is asymptotically stable.

2    Problem 2

Are the following statements true or false? If true, prove the statement. If false, give a counterexample.

1.  Assume X, Y ∈ Rn ×n  satisfying XY = YX and x is a generalized eigenvector of X.  Then, Y x is also a generalized eigenvector of X .

2.  Let A ∈ Rm ×n. Then, rank(AAT ) = rank(A).

3.  Let A ∈ R4×6, and its null space is 3-dimensional.  Then, for any b ∈ R4 , the equation Ax = b has a solution.

3    Problem 3

Suppose there are three birds flying in the sky and assume the birds’ speeds are v1 (k), v2 (k) and v3 (k) at moment k, respectively.  Each bird will adjust its speed based on the average of the other two birds’ speeds, i.e. at moment k + 1, the birds’ speeds are

respectively. Assume the initial speeds are v1 (0) = 8m/s, v2 (0) = 9 m/s and v3 (0) = 13 m/s.

1. What are the speeds of the birds at moment k = 1?