Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

AMATH 301 Rahman

Coding Project 10

Due Friday, December 15th at 11:59pm

Problem 1

In real life we are never given a diferential equation to solve.  We must ind the diferential equation based on what we know about the process and physical laws.  Let’s look at the tank problem that we did in Week 8, but this time with a slight twist.

Two tanks with capacities of 10 liters initially contain 2 grams of salt and 1 liter of water. Water containing 1 g/L of salt enters the irst tank at a rate of 2 L/hour, and the well-mixed solution lows out of the irst tank into the second tank at a rate equivalent to the volume of the irst (i.e., V1  L/Hr).  None of the brine lows out of the second tank.

To model the process follow the steps in the lecture for each tank separately. Notice that the rate for the second tank will depend on the irst.

(1) Model the problem for the volume in liters as an IVP(s) and by using  ode45  (for  MATLAB) or solve_ivp (for Python) solve the IVP (ODE + IC) for the volume of water in the tanks.  Solve from time t = 0 to t = 6 with Δt = 0.01.  Save the volume of the irst tank at each time as a 601 × 1 column vector named A1 and the volume of the second tank at each time as a 601 根 1 column vector named A2.

(2) At what time to the nearest integer does the water start overlowing (hint: use the round function)? Save this integer value as A3. And which tank does it overlow from (1 or 2)? Save this integer value as A4.

(3) Model the problem for the amount of salt in grams as an IVP(s) and by using ode45 (for MATLAB) or solve_ivp (for Python) solve the IVP (ODE + IC) for the amount of salt in the tanks.  Solve from time t = 0 to t = 6 with Δt = 0.01.  Save the amount of salt of the irst tank at each time as a 601 × 1 column vector named A5 and the amount of salt of the second tank at each time as a 601 × 1 column vector named A6.

(4) What is the salt concentration when tank that overlowed in part (b) is completely full of brine?  Save this salt concentration (remember it’s amount/volume) as A7.

Problem 2

Suppose the initial probability ofinding a quantum particle on the line from x = -1 to x = 1 is a compact Gaussian. The particle has equal probability of going to the left or to the right, and has the ability to leave the region. What is the probability that the particle is located at x = 0.5 at t = 1?

This can be solved via the following PDE:

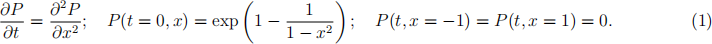
We will use the Crank-Nicolson scheme to numerically solve the problem.

(1) Following the inite diference process we used in lecture, use a second order diference scheme to approximate Pxx  and rewrite this as a linear system of equations Ax = b.  Here the matrix A will be the usual tridiagonal matrix from inite diferences, and the vector b will change at each timestep. Use Δt = 0.01 and Δx = 0.01.  Save a copy of A in a variable named A8.  Save a copy of b as a 199 × 1 column vector after the irst iteration in a variable named A9.

Solve this linear system at each time t  =  [0:0.01:1] using Gaussian elimination (the backslash operator in MATLAB or the solve function in python). Save a copy of b as a 199 × 1 column vector after the last iteration in a variable named A10.

Save the probability ofinding the particle at x = 0.5 at t = 1 as A11.  Find the exact probability of inding the particle at x = 0.5 at t = 1 and save it as A12 (Hint:  do you see a pattern as you iterate the problem?)

Problem 3

Download the iles CP5_M1. mat, CP5_M2. mat, CP5_M3. mat from our Canvas page. Then load the iles onto MATLAB with the following commands:

load  CP10_M1. mat

load  CP10_M2. mat

load  CP10_M3. mat

or Python with the following commands:

After running these commands the variables M1, M2, and M3 will be deined. It is your task to igure out which one represents each of U, S and V. [Hint:  You should be able to see a clear picture].  After you ind which matrices are U, S, and V, let data = USVT .

(1) Calculate how many megabytes it would take to store the matrix data. That is, calculate how many entries there are in this matrix and multiply by 8  /  1e6.  Save your answer in a variable named A13.

(2) Find the number of singular values that capture more than 99% of the information in this image.  That is, ind the smallest value of k such that

Ek  = (m * k + k + n * k)/(m * n) > 0.99,

where m is the number of rows and n is the number of columns of data.  Save the number you found for k in a variable named A14.

(3) Calculate how many megabytes it would take to store this new matrix using the formula from lecture. Save your answer in a variable named A15.

(4) Use the Week 10 coding lecture to guide you in displaying the image that this SVD encodes using the uint8 and imshow commands on MATLAB. Save the integer corresponding to the word that best describes this image as A16.

1) porter, 2) pig, 3) proit, 4) quiet, 5) quicksand, 6) cast, 7) quince, 8) fang, 9) aftermath, 10) experience, 11) ticket, 12) linen, 13) creator, 14) look, 15) trouble, 16) teeth, 17) dog, 18) arm, 19) basin,  20) toad,  21) dinner,  22) position,  23) snail,  24) snake,  25) alarm,  26) ocean,  27)  act,  28) argument, 29) cable, 30) cattle, 31) ink, 32) reward, 33) pump, 34) university, 35) church, 36) kittens, 37) government, 38) umbrella, 39) doll, 40) office worker, 41) spring, 42) bird

It may also be instructive to reconstruct the image using 1,2,3,...  of the singular values and see how many are really needed to fully capture the image. Since this part is subjective, it will not be part of the submission.