Econ 521, Problem Set 10
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Econ 521, Problem Set 10
Please hand in your solutions on Canvas by 11:59pm on Thursday, December 7
Problem 1. Binary education signaling.
In class, we have seen the job-market signaling game with two types and a continuum of education levels. Let us revisit the game, but with a continuum of types θ, uniformly distributed on [0,¯ϑ] for some value ¯ϑ > 0, and two exogenous education levels eH > eL. After observing the chosen education level e, the employer will offer a wage w(e). As in class, ex-post utilities are u1(ϑ, e, w) = w − eϑ and u2(ϑ, w) = −(w − ϑ) 2 . Recall that the employer’s best response to beliefs µ is w = Eµ[θ]. You don’t need to show this again.
Similarly to Bayesian games with a continuum of types and binary actions, we will obtain equilibria in cutoff strategies, that is, the job seeker’s strategy is of the form
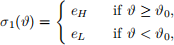
for some cutoff ϑ0. Because type ϑ0 has prior probability 0, it does not matter whether ϑ0 chooses eH or eL.
a. For which values of ¯ϑ, eH, and eL does there exists a perfect Bayesian equilibrium in cut-off strategies, i.e., with a cutoff ϑ0 in the interior of [0, ¯ϑ]? Find the equilibrium.b. Is the equilibrium you found in (a) a separating equilibrium? Explain.
Problem 2. Final-table deals.
The biggest high-roller poker tournament to date was the Triton Million in 2019, in which 54 players bought in for £1m each. First place was scheduled to win w1 = £19m, whereas second place was supposed to receive w2 = £11.67m. The tournament ended with a deal among the last two players once everybody else was eliminated. At the time of the deal, Bryn Kenney had 44.2m in chips, whereas Aaron Zang had 9.8m. They agreed to a deal in which Bryn Kenney received £16,890,509 and Aaron Zang received £13,779,491.
Let µi denote player i’s subjective beliefs that they will win the tournament at the time they made the deal. We will use player i’s subjective expected utility, given those beliefs, as the disagreement point in a Nash bargaining game. Suppose that both players are risk averse with ui(x) = √ xi , where xi is the money player i receives.
Hint: Use variables w1, w2, and p = w1+w2 for the derivations and evaluate the final answer with a computer.
a. What is the set of alternatives U? What is the disagreement point as a function of µK and µZ?
b. For which disagreement points does the actual deal coincide with the Nash bargaining solution? You can state the answer in terms of utilities dK and dZ rather than beliefs µK and µZ.
Hint: Use the characterization through isosceles triangles.
c. The independent chip model (ICM) postulates that two equally skilled players win with a probability that is proportional to their share of chips. If we assume that the players used the Nash bargaining solution to arrive at their deal, can we reject either player’s belief in ICM? Explain.
Almost all poker tournaments (except the WSOP) facilitate final-table deals so that players do not have to make under-the-table arrangements where they could be betrayed. This suggests that utilities are truly non-transferable, and that the Kalai-Smorodinsky solution may be the more suitable solution concept.
d. Find is the Kalai-Smorodinsky solution for disagreement point d = (dK, dZ) given by dK = 3997.0567 and dZ = 3587.2318. What is the Kalai-Smorodinsky split of the pot?
e. What subjective beliefs generate this disagreement point?
2023-12-07