Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Econ 521, Problem Sets 8 and 9

This problem set has the same weight and about the same length as two problem sets.

Please hand in your solutions on Canvas by 11:59pm on Tuesday, November 28

Problem 1. Trading favors.

In order to survive in the political world of Westeros, Varys and Littlefinger each need a favor from the other here and there. Call the person that needs the favor the Requester, the other the Responder. The Requester can either (A)sk for a favor at a small cost ε > 0 or choose (N)ot to do so.  If asked, the Responder can (G)rant the favor at a personal cost c ∈ (ε, 1) or (N)ot. If the favor is granted, the Requester gets a benefit of 1 + ε so that the total utility for a granted favor is 1. The two are playing the following stage game, where in each period, independently from anything else, Varys is the requester with probability p ∈ (0, 1):

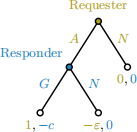
Both people discount future utilities at discount factor δ ∈ (0, 1).

a. Find the subgame-perfect equilibrium of the stage game.

b. Suppose that the game is finitely repeated, i.e., there are a total of T < ∞ opportunities to grant favors. Is there a subgame-perfect equilibrium in which a favor is granted?

c. Suppose that the game is infinitely repeated. Let σG  denote the grim-trigger strategy profile, in which players play (A, G) for as long as (A, G) has been played in every period, and (N , N) otherwise. Under what conditions on the parameters, c, p, and δ is σG  a subgame-prefect equilibrium?

d. Perform comparative statics on the equilibrium in (c).  For which values of c, p, and δ is it easier to sustain cooperation?

Problem 2. Perfect Bayesian equilibrium.

Consider the following extensive-form game:

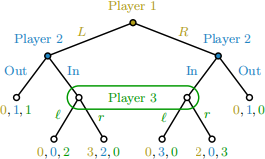
a. Is this a game of perfect recall? Justify your answer.

b. Find all perfect Bayesian equilibria of the game. Hint: Verify consistency backwards through the tree, i.e., distinguish cases based on Player 3’s mixing probabilities.

Problem 3.  Cyberdefense.

The Government selects its defensive strategy against potential cyber attacks. In doing so, the government may either be competent (ϑC ) or incompetent (ϑI ). The government is aware of its type and selects whether to (I)nvest or (N)ot invest into its cyberdefense.  A group of Hackers observes the Government’s decision to invest and decide whether to launch an (A)ttack or (N)ot. The Hackers do not know the Government’s type, but only know that a fraction μ0  of Governments are competent. The attack is successful either if the Government is the incompetent type ϑI  or if it does not invest.  Utilities are as follows:

a. Simplify the problem by eliminating strictly dominated strategies.

Hint:  Start from the end of the game  tree and work your way backwards through the tree.

b. Find all perfect Bayesian equilibria of this game, given prior beliefs μ0 .

c. Explain the intuition behind the perfect Bayesian equilibria by distinguishing whether the Hackers starts with optimistic or pessimistic prior beliefs.

d. Is this a signaling or a cheap-talk game? Explain.