Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Computer Science

Summative Assignment

Linear Algebra

Marks will be given for correct solutions and, where appropriate, solutions that gen- eralise well.

1.  Consider the set of all lists of numbers in which all the numbers in the list are distinct, i.e.  no number occurs more than once within the list.  We will call this set  LNR  (lists  with no repeats).   Also  consider  the  operation  □ which takes two lists of numbers and concatenates them, but recursively re- moves any two identical adjacent numbers after concatenation.  For example [1, 2, 3]□[4, 5, 6] = [1, 2, 3, 4, 5, 6] and [1, 2, 3, 4]□[4, 3, 5, 6] = [1, 2, 5, 6].  State, with justification, whether □ acting on LNR

(a) has an identity element

(b)  has an inverse operation

(c) has associativity

(d) has commutativity

(e)  forms a group [10 marks]

2.  Find all unit vectors u ∈ R3  that are orthogonal to both v1  = (3, 0, 4) and v2  = (−5, 8, 2).  Give your answer in an exact form (not as a decimal) and explain your reasoning.                                                                       [10 marks]

3.   (a)  Draw the result of applying the shear transformation T1 , represented by the matrix

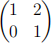
to the unit square with corners {(0, 0), (1, 0), (1, 1), (0, 1)}        [2 marks]

(b) Write down the matrix representing T2 , a rotation through 45。clockwise, leaving your answer in exact form. [2 marks]

(c) Write down the matrix representing T3  where

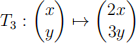[2 marks]

(d)  Find the area of the shape resulting from applying T1  then T2  then T3  to the circle of radius 1 centred at (1, 0).  Justify your answer.       [4 marks]

4. Find and look through the paper [1] (including the Appendix), which talks about visualisation of high-dimensional vectors that represent genetic infor- mation. You should not expect to understand all of it, but you should find some of the concepts familiar from your study of linear algebra.

(a) Which of the concepts introduced in the linear algebra submodule (from the concept diagram) are referred to in this paper, and on which page? Marks will be awarded for each distinct concept you correctly identify. Marks will be deducted for incorrect identification of concepts. [12 marks]

(b)  Choose one of these concepts and explain, in your own words, how it is  used in the paper.         [4 marks]

(c)  Find in the paper an example of a linear combination: write it down, say

where it is in the paper and justify why it is a linear combination.  Also find a non-linear function, write it down, say where it is, and justify why it is non-linear.          [4 marks]

References

[1]  Han Li, Peter Ralph, Local PCA Shows How the Effect of Population Struc- ture Differs Along the Genome, Genetics, Volume 211, Issue 1, 1 January 2019, Pages 289–304, https://doi.org/10.1534/genetics.118.301747

Calculus

In these questions the set of natural numbers includes zero: N = {0, 1, 2, ...}.

5.  For each of the following functions, state whether it is an injection, surjection, bijection or none of these, and prove your answer.

(a)  f : R →7 R, where f(x) = |3x − 15| .

(b)  f : Q →7 N, where f(x) = x/5 rounded down to the nearest integer. (c)  f : R →7 R × R, where f(x) = (x3 , |x|).

(d)  f : (0, 1) →7 (6, ∞), where f(x) = 1/x + 5. [8 Marks]

6. I gave ChatGPT the prompt  “Give me  an obscure example of a bijection” and got the following response (note: ‘one-to-one’ means injective, and ‘onto’ means surjective):

An obscure example of a bijection is the function that maps each positive in- teger to a corresponding positive integer such that the sum of the digits of the original number is equal to the sum of the squares  of the  digits of the mapped number. This function takes each positive integer n to another positive integer m, where m is determined by the following process:

(a)  Take the decimal representation of n, for example, n = 315 .

(b)  Calculate the sum of the squares of its digits: 32 +12 +52  = 9+1+25 = 35 .

(c)  Find a positive integer m where the sum of the  digits of m is  equal to the result from step 2.  In this case, m = 899, as8 + 9 + 9 = 35 .

This function is a bijection because it is a one-to-one correspondence between the positive integers, and it is also onto because every positive integer n  can be mapped to a corresponding positive integer m in this way. It’s quite  obscure and not commonly encountered in everyday mathematics.

Discuss whether ChatGPT has given a good answer to my prompt, justifying any claims you make.                   [2 Marks]

7.  I asked Bard for an example of a bijection and got the following response:

Here is an example of a bijection:  f(x) = x2

This function is injective  because for  every  element in  the  domain  (the  real numbers),  there  is  a  unique  element  in  the  codomain  (the  non-negative  real numbers)  that it maps  to. It is  also  surjective  because  every  element  in  the codomain is mapped to by at least one element in the domain.

Discuss whether Bard has given a good answer to my prompt, justifying any claims you make.                 [2 Marks]

8. Prove by induction that for all n ∈ N if f(x) = axn  then f′ (x) = anxn−1 .

You may assume the product rule for differentiation.                         [9 Marks]

9. Locate the critical points of the function

f(x,y) = x2y2  − 3y2 x − x2 − y2 + 3x − y + 7

and classify them as (local) minima, maxima or saddle points.        [14 marks]

10. Let f(x1 , x2 , x3 ) = x1(3)x2(2) − cos(x1 x3 ) − x2 max{x1(3)x2(2), x1 x3 }.

(a) Draw a computation graph for f, identifying intermediate variables.  List the intermediate variables and the operation by which each is obtained from its inputs.

(b)  Compute the partial derivatives of each intermediate variable with respect to its inputs.

(c) Use forward mode Automatic Differentiation (AD) to compute the direc- tional derivative of f at point (π,−1, 1/2) in the direction (1, −2, −2)T . Show your working.

(d)  Use reverse mode AD to compute a vector pointing in the direction of greatest increase in f from point (π,−1, 1/2). Show your working. [15 marks]