Math 475 Exam 1, Fall 2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Math 475
Exam 1, Fall 2023
1. In how many ways can we place four green rooks and five orange rooks on a 12 by 12 chessboard, such that no two rooks are attacking?
2. Find a positive integer n such that

3. Find an integer t such that 0 ≤ t ≤ 87 and t ≡ 2 (mod 8) and t ≡ 6 (mod 11).
4. Suppose we are given integers m ≥ 2 and n ≥ 2. Recall the Ramsey number R = R(m, n). Consider a room full of people. Assume that there are exactly R persons in the room. Assume that any two people in the room are either friends or enemies. Show that either:
(i) there exist m people in the room such that any two are friends; or
(ii) there exist n people in the room such that any two are enemies.
5. For nonnegative integers i, j define
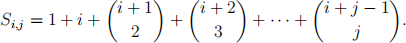
(i) (3 points) Find S0,4, S1,3, S2,2, S3,1, S4,0.
(ii) (3 points) Find Si,j for all i, j (express Si,j in terms of i, j).
(iii) (4 points) Prove that your answer to (ii) is correct.
6. For an integer n ≥ 1 define

where the sum is over all sequences of nonnegative integers r, s, t such that r + s + t = n.
(i) (4 points) Find F1, F2, F3, F4.
(ii) (2 points) Find Fn in closed form.
(iii) (4 points) Prove your answer to (ii) is correct (feel free to invoke results from the textbook to support your argument).
7. For an integer n ≥ 0 define

(i) (4 points) Find S0, S1, S2, S3, S4.
(ii) (2 points) Express Sn in closed form.
(iii) (4 points) Prove that your answer to (ii) is correct for all n.
8. Define a partial order ≤ on the set X = {2, 3, 4, 6} such that a ≤ b whenever a divides b (a, b ∈ X). Find all the linear extensions of this poset.
9. Let n = 18 and consider the set X = {1, 2, . . . , n}. Recall that each permutation a1a2 · · · an of X has a unique inversion sequence b1b2 · · · bn. (5 points) How many permu-tations a1a2 · · · an of X have an inversion sequence b1b2 · · · bn such that b5 = 8? (5 points) Prove that your answer is correct (feel free to invoke results from the textbook to support your argument).
10. For an integer n ≥ 1, consider the set {1, 2, . . . , n}. For a subset A of {1, 2, . . . , n} define the weight of A to be the integer
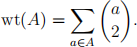
Define the integer
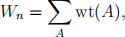
where the sum is over all the subsets A of {1, 2, . . . , n}.
(i) (3 points) Find W1, W2, W3.
(ii) (3 points) Find Wn for n ≥ 1 (express Wn as a function of n).
(iii) (4 points) Prove that your answer to (ii) is correct.
2023-12-02