EECE7204 Problem Set 4
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
EECE7204
Problem Set 4
Problem 1 (3.32). The length of time, Z, an airplane can fly is given by Z = αX, where X is the amount of fuel in its tank and α > 0 is a constant of proportionality. Suppose a plane has two independent fuel tanks so that when one gets empty the other switches on automatically. Because of lax maintenance a plane takes off with neither of its fuel tanks checked. Let X1 be the fuel in the first tank and X2 the fuel in the second tank. Let X1 and X2 be modeled as uniform i.i.d. RVs with pdf fX1 (x) = fX2 (x) = 1/b [u(x) − u(x − b)]. Compute the pdf of Z, the maximum flying time of the plane. If b = 100, say in liters, and α = 1 hour/10 liters, what is the probability that the plane will fly at least five hours?
Problem 2 (3.34). Given two random variables X and Y that are independent and uniformly distributed as U(0, 1):
(a) Find the joint pdf fUV of random variables U and V defined as:

(b) Sketch the support of fUV in the (u, v) plane. Remember support of a function is the subset of its domain for which the function takes on nonzero values.
Problem 3 (3.35). Let X and Y be independent, uniformly distributed RVs, both with pdf fX(x) = 1/2, |x| < 1 and zero otherwise, and fY (y) = 1/4, |y| < 2 and zero otherwise. Compute (a) the pdf of Z = X + Y ; (b) the pdf of Z = 2X − Y .
Problem 4 (3.37). Consider the transformation
Z = aX + bY
W = cX + dY.
Let
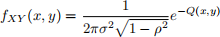
where

What combination of coefficients a, b, c, d will enable Z, W to be independent Gaussian RVs?
Problem 5 (3.40). Consider the transformation
Z = X cos θ + Y sin θ
W = X sin θ − Y cos θ
Compute the joint pdf fZW (z, w) in terms of fXY (x, y) if
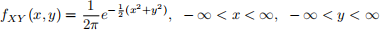
(It may be helpful to note that this transformation is a rotation by +θ followed by a negation on W.)
2023-12-02