COMP2121 (1B) Discrete Mathematics Assignment 4: Graphs
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Assignment 4: Graphs
COMP2121 (1B) Discrete Mathematics
Release date: October 27, 2023
Due date: November 28, 2023
Learning Outcomes:
O1 Understand abstract mathematical concepts
O2 Perform abstract thinking
O3 Analyse and enumerate
Question 1 (35 Points): Basics on graphs (O1,O2,O3)
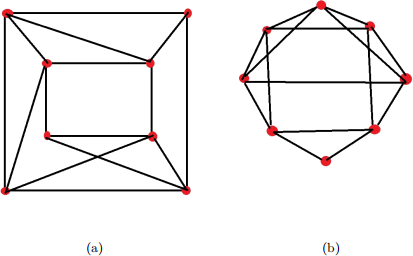
a) (5 Points) Two graphs G1 = (V1 , E1 ) and G2 = (V2 , E2 ) are isomorphic if there is a 1 - 1 correspon-dence function f : V1 ! V2 such that (u, v) 2 E1 if and only if (f(u), f(v)) 2 E2 . Determine whether the following two graphs are isomorphic and justify your answer. Note that vertices are illustrated as red dots.
b) (5 Points) At a party everyone shakes hand with each other exactly once. The total number of handshakes is 1225. How many people are there at the party?
c) (5 Points) Draw a simple, connected, undirected graph consisting of 1 vertex of degree 1, 3 vertices of degree 3, and 4 vertices of degree 4. Is the graph you draw planar or not? Justify your answer.
d) (5 Points) Determine whether there are Euler trails in the following graphs. Justify your an- swer. i) Figure III; ii) Figure IV; iii) The graph you plotted in Question 1 c).
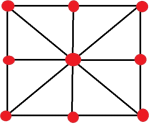
Figure III
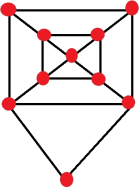
Figure IV
e) (5 Points) Draw a simple, planar graph whose region coloring number is equal to four.
f) (5 Points) A simple, undirected graph with 20 vertices and 10 edges has no cycle. Can you de- termine its (vertex) coloring number? Explain your answer.
g) (5 Points) The longest trail of a graph is a path with maximal length and no repeated edges. Show that if a simple, undirected, connected graph G has exactly two distinct longest trails, they (the two trails) must share at least one vertex in common.
Question 2 (30 Points): Graph Counting Problems (O3).
a) (5 Points) Determine the number of cycle subgraphs with 10 vertices in the following graph.
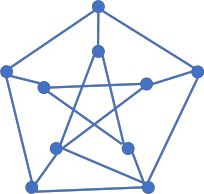
b) (10 Points) A tree is a simple, undirected graph where each pair of vertices are connected by exactly one path. Find all tree graphs whose complement graph is also a tree.
c) (5 points) Deine Dn isa simple undirected graph consisting of n+2 vertices, generated by connecting each vertex in a line graph of n vertices to two non-adjacent vertices. An example D4 is shown below.
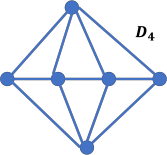
How many ways are there to color Dn with k colors? (n and k are two generic integers larger or equal to 2.)
d) (10 Points) A k-regular graph is a simple, undirected graph where all vertices have degree k. Count (regarding isomorphic graphs as diferent graphs) the number of i) 3-regular graphs with 6 vertices {1, 2, . . . , 6}, ii) connected 2-regular graphs with n vertices {1, 2, . . . , n} for a generic n.
Question 3 (20 Points): Planar graphs. (O1,O2)
a) (10 points). Determine whether the following graphs are planar or not. If they are, verify Euler’s formula; and if they aren’t, give reasons.
i) Figure V (5 Points).
ii) Figure VI (5 Points).
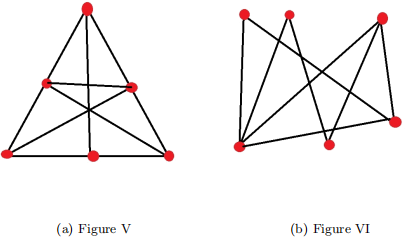
b) (5 Points). Consider a simple planar graph with 16 vertices and 28 edges. Determine the minimum number of regions that the graph can have. Explain your answer.
c) (5 Points). Show that a 3-regular simple, connected, planar graph of more than 4 vertices must have a region whose degree is at least 4.
Question 4 (20 Points): Applications of graph theory. (O2)
a) (5 Points). A group of 24 people are at a party. Each of them is knew at least 15 people at the party. Prove that they can be seated at around table in such away that everyone knows his/her two neighbours.
b) (5 Points). 9 strangers play an ice-breaking game at a party for several rounds. For each round, they will sit around a round table and introduce themselves to their neighbours. The rule is that no one is seated next to his/her acquaintance in a new round.
Suppose the game has been played for 3 rounds. Is it always possible to ind a seating plan for the 4th round? Explain your answer.
c) (10 Points). Let U be the set that contains all persons in the world, and A be an arbitrary subset of U such that jAj = 6. Prove that at least one of the following is true:
i) There exist 3 persons in A who know each other.
ii) There exist 3 persons in A who are all strangers.
2023-11-27