ENEE620. Final examination 2020
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
ENEE620. Final examination, December 16-17, 2020.
Problem 1. (20pt) For n ∈ N consider probability mass functions pk,n, k = 1, . . . , n given by

Let Xk,n, k = 1, . . . , n be i.i.d. RVs with pmf pk,n and define
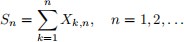
(a) For each n = 1, 2, . . . find EXk,n, Var(Xk,n) for all k = 1, . . . , n.
(b) Does the sequence { Sn/n, n = 1, 2, . . . } converge in probability? If yes, what is the limiting RV?
(c) Consider the sequence

Does it converge in distribution? If yes, what is the limiting RV? (One way to proceed is to use characteristic functions; in particular, what is this function for the Poisson distribution?).
Problem 2. (15pt) Let (Nt)t≥0 be a Poisson process PP(λ). Consider a process
Xt = ξ · (−1)N(t) , t ≥ 0
where ξ is a Bernoulli RV independent of N and such that P(ξ = 1) = P(ξ = −1) = 1/2 (for a given t we flip the coin to find ξ and then compute Xt). Show that EXt = 0 and E[XsXt] = e −2λ|t−s| .
Problem 3. (15pt) Let X1, X2, . . . be a sequence of i.i.d. nonnegative RVs with a continuous CDF F(x). Let Z1 = 1, Zk = min{n > Zk−1 : Xn ≥ max(X1, . . . , Xn−1)}, k ≥ 1 be the sequences of records.
Does the sequence of RVs (Zk)k≥1 form a Markov chain? If yes, find the transition probability matrix of this Markov chain.
Problem 4. (20pt) Let X and Y be two Gaussian RVs with EX = EY = 0, EX2 = EY2 = 1, and E(XY ) = ρ. Show that
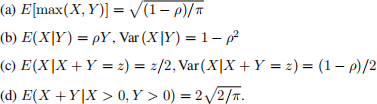
Problem 5. (15pt) Let Zi , i ≥ 1 be a collection of i.i.d. RVs with P(Z = −1) = 3/4 and P(Z = c) = 1/4, where c is a real number. Let Xn = X0 + Z1 + Z2 + · · · + Zn, n ≥ 1, where X0 = 5.
(a) Find a value of c such that the sequence (Xn)n forms a martingale.
(b) For the value of c found in Part (a), is there an RV X such that Xn a.s.→X? Please justify your answer.
(c) For the value of c found in Part (a), is it true that P(∪n≥1{Xn = 0}) = 1 ? Please justify your answer.
2023-11-27