Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

ECE 175 Computer Programming for Engineering Applications

Homework Assignment 4

Conventions: Name your C programs hwxpy.c where x corresponds to the homework number, and y corresponds to the problem number. For example, the C program for homework 4, problem 2 should be named as hw4p2.c

Write comments in your programs. Programs with no comments will receive only PARTIAL credit. For each program that you turn in, at least the following information should be included at the top of the .c file:

● Author:

● Date created:

● Brief description of the program:

– input(s):

– output(s):

– an algorithm (or description/relationship between inputs and outputs)

Relevant Programming Concepts:

● File I/O

● User-Defined Functions

Submission Instructions: Use the designated Drop box on D2L to submit your homework. Submit only the .c files.

1 Compressed File (35 points)

You are given a file named Ascii_Art_Compressed.txt. The file contains integer/character pairs. The integer indicates how many times the character is repeated in decompressed format. For example: the compressed sequence 5A1B2A would translate to an decompressed sequence of AAAAABAA. Note: there are no integers in the decompressed file.

Write a C program that reads all of the integer/character pairs in the compressed file, and writes the decompressed sequences to the file Ascii Art_decompressed.txt.

Note: Also test your code with Ascii_Art_Compressed_2.txt

2 Prime Numbers (35 points)

A number is prime if it has exactly two positive divisors, itself and 1. One way to test if a number n is prime is to check if n is divisible by any number from 2 to 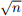 (dividing with numbers larger than 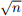has no additional benefit to testing for primality). For instance, consider checking the primality of 17. The square root of 17 is 4.1231, so it is sufficient to test if 17 is divisible by 2, 3, and 4. Since 17 is not divisible by any of those numbers, 17 is deemed to be prime. The first 6 prime numbers are 2, 3, 5, 7, 11, 13.

A proposed method for generating a prime number is starting with any integer n and applying the polynomial P = n²+n+41. Note that this polynomial does not always generate a prime number.

1. Develop a function called isPrime that receives as input long long int P and returns 1 if P is a prime number and 0 otherwise. Use the following function prototype:

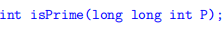
2. Write a main function that loops n (starting from n = 0) and checks if P is prime, where P = n² + n + 41. Stop the loop after 200 prime numbers are found.

3. Print the output to the file PrimesFound.txt. A portion of the output file is

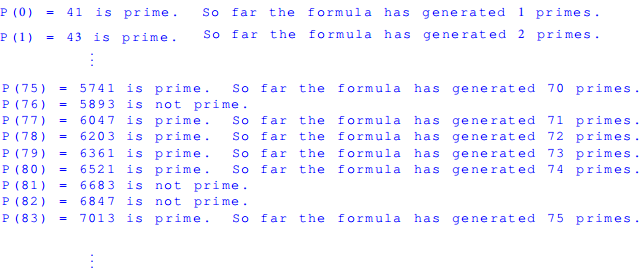
Lab 4 assignments (30 points): You will complete lab 4 during the week after you submit homework 4.