CSC/MATA67 Assignment 3 - Combinatorics, Strong Induction and PHP
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CSC/MATA67 Assignment 3 - Combinatorics, Strong Induction and PHP
Due: Nov 20, 2023 at 11:59 p.m.
Submit your assignment by the due date to Gradescope. Recall that the rules of academic integrity for this class allow you to work with one other person.
You must list your partner on Gradescope and only one of you submits the assignment.
You may not use any other sources such as the internet or other textbooks to ind solutions to these questions. Your answers will be graded both on their inal solution as well as the work you show to achieve that solution. Note that a subset of the questions will be graded. By submitting your assignment you agree to abide by these rules.
1. Let H(n) be deined as follows:
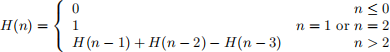
Prove that An 2 N, n ≥ 1 ! H(2n) = H(2n - 1) = n using strong induction. Hint: You may want to split this into two steps.
2. How many integers must be selected from the set of integers from 2 through 40, to ensure there are at least two integers with a common divisor greater than 1.
3. A certain college class has 40 students. All the students in the class are known to be from 17 through 34 years of age. You want to make a bet that the class contains at least x students of the same age. How large can you make x and yet be sure to win your bet?
4. How many permutations are there of the letters in the word POLYUNSATURATED?
5. How many arrangements of the letters in the word SOCIOLOGICAL have no consecutive O’s?
6. (a) How many ways can seven people be seated around a circular table?
(b) If two of the people insist on sitting next to each other, how many arrangements are there?
(c) If two of the people insist that they cannot sit beside each other, how many arrangements are there?
7. In this question we are considering 5 card poker hands (cards are unordered). How many hands:
(a) contain 4 aces?
(b) contain cards of exactly two suits?
(c) contain cards of all suits?
(d) contain two pairs?
8. How many ways can 15 students join 5 diferent clubs? You can assume any student will join one club. How does this change if now we require that each club have 3 students?
9. Suppose you roll a six sided die three times and record the outcome as an ordered list of length 3 (for example, if you roll 4, 4, 5 you would write this as 445). In this question you will want to use the Inclusion-Exclusion Principle of Sets.
(a) How many possible outcomes are there where there is exactly one 6?
(b) How many possible outcomes are there when there is exactly one 1 or exactly one 2? How many ways if we consider this for inclusive OR? how many for exclusive OR?
(c) How many possible outcomes are there where there is exactly one 1 or one 2 or one 6? Use inclusive OR. HINT: You may wish to draw a Venn diagram to help you.
(d) Suppose that 6 numbers are randomly positioned around a circle. Prove that there always exists 3 consecutive numbers around the circle whose sum is at least 11. Use the Pigeon Hole Principle for this question.
10. If n is a positive integer, how many 4-tuples of integers from 1 through n can be formed in which the elements of the 4-tuple are written in increasing order but are not necessarily distinct? In other words, how many 4 tuples of integers (x1 , x2 , x3 , x4 ) are there with 1 ≤ x1 ≤ x2 ≤ x3 ≤ x4 ≤ n.
HINT: Try to relate this to the donut problem. what does the 4 represent in the donut problem? what does the n represent in the donut problem?
11. Provide a combinatorial argument to show that if s and t are positive integers with s = 5t, then
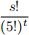
is a positive integer.
What is a combinatorial argument? try to relate this expression to permutation or combinations. Your answer should not include a lot of algebra (i.e., you should not try to multiply out the factorials to simplify). It should be a simple argument using a couple sentences and the material that we’ve learned so far.
12. Provide a combinatorial argument to show that if n is a positive integer, then
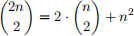
You will only get marks for this question if you use a combinatorial argument. See Q11. for a description of combinatorial argument.
13. You are eating Smarties. You have decided to limit yourself to merely 20 smarties. There are 6 colours in the box; red, orange, yellow, mauve, pink and brown.
(a) Assuming there are more than 20 smarties of each colour, in how many diferent colour combina- tions can you choose your smarties from the box.
(b) Assuming there are more than 20 smarties of each colour, in how many diferent colour combina- tions can you choose your smarties such that you have at least 3 red ones.
(c) Now suppose that there are only 10 of the red smarties in the box but at least 20 of the other colours. Now how many diferent colour combination are there for you to choose your 20 smarties?
14. This question is a little more challenging. How many integers in the interval [1, 9 999] (i.e., the integers between 1 and 9 999 inclusive) have digits whose sum is 10. For example, 46 lies within the interval and 4 + 6 = 10, similarly for 9001, as 9 + 0 + 0 + 1 = 10 but the digits of 812 do not sum 10.
2023-11-19