EE7401 Homework 3
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
EE7401 Homework 3
Instructions:
● Please write your final solutions in the boxes shown below, then scan (if needed) and upload via NTULearn/Assignments/Homework3 by 23:59, 14 November 2023.
● Please do not copy from others, or let others copy your solution.
● Penalties may apply for late submission.
● Homework 3 carries 10% overall marks.
Q1) When did you start your simulations: Consider the simulation of a first order auto- regressive, or AR(1), process. A wide-sense stationary real white noise process x[n] with autocorrelation Rxx [m] = 5δ[m] is passed through the AR(1) filter with a = 0.5, such that the output is y[n] = x[n] + 0.5y[n − 1].
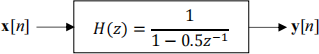
1.1) (1.1.a) Assume the above filter operates at all times. Then y[n] is jointly wide-sense stationary. Find the cross-correlation between x[n] and y[n], Rxy [m] = E{x[n1]y[n2]}, where m = n1 − n2. [Hint: There are many ways to solve this problem. You may use the frequency domain or the z domain approach, finding Sxy (ω) or Sxy (z) first, and then taking the inverse Fourier or z transform. You may express y[n] as a convolution of x[n] with ℎ[n] (impulse response), multiply the equation by x[n1], and take the expectation.]

(1.1.b) Find the autocorrelation of the AR(1) process, Ryy [m].

(2 marks)
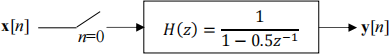
1.2) Part (1.1) results are true if the simulation is started at n = −∞. However, real-life simulations start at finite times. Consider a real-life simulation of the same AR(1) process as above, where the simulation starts at n = 0. x[n] is still the same wide-sense stationary with the same autocorrelation. However, the AR(1) filter starts at n = 0 (meaning, there was no filter before n = 0, or the output was zero). Therefore, the output becomes y[n] = 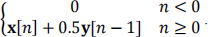 Note that y[n] is no longer stationary. Therefore, the
Note that y[n] is no longer stationary. Therefore, the
auto/cross-correlations involving y[n] no longer depend on the time difference m but depend on both times, like Ryy [n1,n2]. As a result, the power spectrums of y[n] do not exist, and the power spectrum based approaches can no longer be used to find the auto/cross-correlations. The time-domain approach may still be used.
(1.2.a) Express y[0] using only the input x[0]. Express y[1] as a sum of only input terms of the form x[k]. There should not be any past output term such as y[n − 1]. Continuing as above, express y[n2] for any n2 ≥ 0 as a sum of only input terms of the form x[k]. There should not be any past output term such as y[n2 − 1].

(3 marks)
(1.2.b) Find the cross-correlation between x[n] and y[n], Rxy [n1,n2] = E{x[n1]y[n2]}, for all n1,n2 ≥ 0 by multiplying eq.(1) by x[n1], and taking the expectation of both sides. [Hint: Find 2 cases: write answers in 2 left boxes, and write the cases in 2 right boxes.]

(4 marks)
(1.2.c) Extend your result of (1.2.b) to all possible n1,n2 values. [Hint: Find 2 cases: write answers in the 2 left boxes, and write the condition of the primary case in the right box.]

(2 marks)
(1.2.d) Find the autocorrelation of the AR(1) process, Ryy [n1,n2] for all possible n1,n2 values. [Hint: Replace both y[n1] and y[n2] in E{y[n1]y[n2]} by eq.(1) twice, then take the expectation of this double summation. You should find 3 cases (it is possible to combine 2 primary cases into a single case): write answers in the 3 left boxes, and write the conditions of 2 primary cases in the 2 right boxes.]

(1.2.e) For all non-negative n1 and n2, is Rxy [n1,n2] of (1.2.c) equal to Rxy [m] of (1.1.a)? If not, when are they equal?
For all non-negative n1 and n2, is Ryy [n1,n2] of (1.2.d) equal to Ryy [m] of (1.1.b)? If not, when are they equal?
(4 marks)
Q2) Bandlimited process does change with time: In lecture we have upper bounded the change in value of a bandlimited process over a small time τ. Here we obtain a lower bound (and a new upper bound). First, two intermediate results are obtained as below.
2.1) Assume that the time is bounded by |τ | < (π/σ) and that the frequency is bounded by |ω| ≤ σ. Then, using the fact that if 0 < φ < (π/2), then (2φ/π) < sin φ < φ , find a lower bound and an upper bound on sin 2(ωτ/2) :
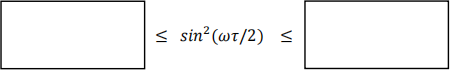
(4 marks)
2.2) Let the power spectrum of x(t) be Sxx (ω). If x(t) is passed through a differentiator (frequency response H(ω) = jω), then you have already found SxIx I (ω), the power spectrum of the output x′ (t), in terms of Sxx (ω), in Homework 2 Q(2.b). Copy this SxIx I (ω) below to obtain the autocorrelation of the output x′ (t) as

Now, putting τ = 0, the average power of the output x′ (t) is:

(2 marks)
2.3) (2.3.a) Express the expectation of the square of the change in x(t) over time τ , E{|x(t + τ) − x(t)|2}, using its autocorrelation:

(5 marks)
(2.3.b) Use (2.3.a), 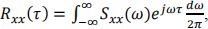 and 1 − cosθ = 2sin2(θ/2), to get:
and 1 − cosθ = 2sin2(θ/2), to get:
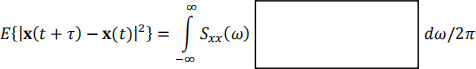
(4 marks)
(2.3.c) Let us say the integral you obtained in part (2.3.b) is 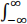 Sxx (ω)g(ω)dω/2π for some function g(ω) that you wrote inside the box. Now, since x(t) is bandlimited, its power spectrum Sxx (ω) = 0 for |ω| > σ . Therefore, this integral’s limits maybe changed, E{|x(t + τ) − x(t)|2} =
Sxx (ω)g(ω)dω/2π for some function g(ω) that you wrote inside the box. Now, since x(t) is bandlimited, its power spectrum Sxx (ω) = 0 for |ω| > σ . Therefore, this integral’s limits maybe changed, E{|x(t + τ) − x(t)|2} = 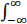 Sxx (ω)g(ω)dω/2π =
Sxx (ω)g(ω)dω/2π = 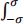 Sxx (ω)g(ω)dω/2π . Apply the lower and upper bounds on sin 2(ωτ/2) from part (2.1) to obtain the lower and upper bounds on the expectation:
Sxx (ω)g(ω)dω/2π . Apply the lower and upper bounds on sin 2(ωτ/2) from part (2.1) to obtain the lower and upper bounds on the expectation:

(4 marks)
(2.3.d) The difficulty is that, unlike in the lecture, we can’t replace ω by σ in the lower bound. Therefore, we need to evaluate 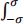 Sxx (ω)ω2dω/2π . This has already been done in part (2.2) using the differentiated process x′ (t). Use the result of (2.2) on the lower and upper bounds of (2.3.c) to obtain the final result:
Sxx (ω)ω2dω/2π . This has already been done in part (2.2) using the differentiated process x′ (t). Use the result of (2.2) on the lower and upper bounds of (2.3.c) to obtain the final result:
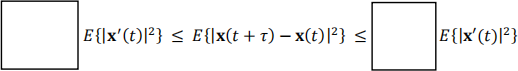
(2 marks)
(2.3.e) Is the upper bound of (2.3.d) smaller, or larger, than the upper bound found in the class?
(4 marks)
2023-11-11