Econ 700 Midterm 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Econ 700 Midterm 2
10 November 2022
Answer the following questions to the best of your ability. Please write everything that you want to be graded in your bluebook. Do not provide irrelevant information. If a question seems ambiguous to you, state the most reasonable assumptions to resolve the ambiguity and proceed on that basis. Show your work and explain your reasoning. Use the definitions of concepts that we have developed in class. If you would like to use an alternate definition, you should show that your definition is equivalent to the one we have used. If we have stated a theorem in class, you may use it without proving it unless I explicitly ask you to prove it. If a theorem was stated only in homework, you will need to prove it in order to use it. No notes are allowed. Label clearly which question you are answering. There are 100 total points available.
1. (24 points) Please state whether each of the following statements is true or false. Prove the true statements and disprove the false statements.
(a) For every real-valued function f : R2 → R, if (x0 , y0 ) ∈ R2 and 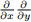 f(x0 , y0 ) exists, then
f(x0 , y0 ) exists, then 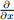 f(x0 , y0 ) also exists.
f(x0 , y0 ) also exists.
(b) If G : R2 → R is continuously differentiable and if G(x,y) = 0 defines y as a function of x in an open ball centered at (x0 , y0 ) ∈ R2 , then G(x,y) = 0 also defines x as a function of y in a (possibly different) open ball centered at (x0 , y0 ).
2. (19 points) Let f : Rn → Rm ;x |→ f(x) and g : Rm → R;y |→ g(y) be twice continuously differentiable functions. Recall that the composition function g ◦ f : Rn → R is defined by (g ◦ f)(x) = g(f(x)).
(a) Express D(g ◦ f)(x) in terms of the Jacobian/Hessian matrices of f and g. (b) Define G : Rm → Rm by G(y) = [Dg(y)]T . Show that DG(y) = D2g(y).
(c) Define ϕ : Rn → Rm by ϕ(x) = [Dg(f(x))]T . Express Dϕ(x) in terms of the Jaco- bian/Hessian matrices of f and g.
3. (19 points) Find all critical points of g(x,y) = x2 + 4y2 − 4xy + 2 and check the second order conditions at each critical point to determine what local maxima and minima exist for this function.
4. (19 points) Show that for any positive integer k, for any b > 0, and for some c ∈ (0, b), we have that
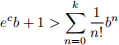
5. (19 points) Solve the following problem by checking the NDCQ, finding the first order condi- tions, finding all critical points, and determining which critical points are global maximizers:
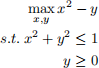
2023-11-10