MAE 280A Linear Systems Theory Fall 2023 Homework #2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MAE 280A Linear Systems Theory
Fall 2023
Homework #2
Due on Friday, Nov 10th before 11:59 p.m. PST, submit through Gradescope. Make sure to select the appropriate questions for your answers to receive credit and include all your work/code for full credit.
Exercise 1 (Lipschitz continuity)
1. (2 points) X and Y are subsets of Rn and Rm respectively and f : X → Y and g : Y → Rp are two Lipschitz continuous functions. Is the composition of g and f, i.e., g 。f, Lipschitz continuos? Prove it or give a counterexample.
2. (2 points) Let f : Rn → Rm and g : Rn → Rm be two functions that are Lipschitz con- tinuous. Is the function f + g Lipschitz continous? Prove it or give a counterexample.
Exercise 2 (Solution to a MDE) Let A1 (t), A2 (t), and F(t), be known piecewise con- tinuous n × n matrices. Let Φi be the transition matrix associated to ˙(x) = Ai (t)x for i = 1, 2 (which comes from the respective matrix differential equation (MDE) seen in lecture). Show that the solution of the following matrix differential equation (with X(t) an n × n matrix):
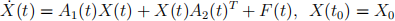
is
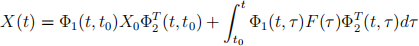
Exercise 3 (State transition matrix properties) Derive an expression for
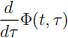
where Φ(t,τ) is the state transition matrix of ˙(x) = A(t)x. Hint: Here τ is a variable that represents the classical t0 .
Exercise 4 (State transition matrices and dynamics)
Find a matrix A(t) such that

is the state transition matrix of ˙(x) = A(t)x
Exercise 5 (Discrete dynamical system) Derive the state transition function for the discrete time dynamical system x[k + 1] = ax[k] with initial condition x[0] = x0 and read out map y[k] = x[k]. Assume a is a parameter in R and x[i] e R. Prove or disprove if the dynamical system is linear.
Exercise 6 (Perturbed dynamical system) A given dynamical system can be modeled as follows
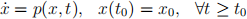
Assume this dynamical system has a solution and it is unique. In presence of a perturbation, this dynamical system can be modeled as
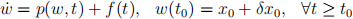
It is known that for t e [t0 , t0 + T], ||f(t)|| 三 ϵ1 and ||δx0 || 三 ϵ0 , determine a bound on ||x(t) - w(t)|| for t e [t0 , t0 + T].
Exercise 7 (Lipschitz continuity and linearization) Consider the inverted pendulum equation with normalized input torque:

where x1 is the angle that the pendulum makes with the vertical, x2 is the angular rate of change, l is the length of the pendulum, and u is a normalized torque input signal.
(a) What is the most you can say about the existence and uniqueness of a solution to this equation, given a fixed input signal u.
(b) Determine the linearized model for the perturbation dynamics about the condition in which the pendulum is pointing straight up with zero velocity.
Exercise 8 (Trajectory and output of a dynamical system) Consider a single-input, single-output, time invariant linear state equation:

where:
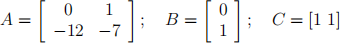
and t0 = 0.
(a) Suppose u(t) = 0 for t ≥ 0. Describe what happens to the output signal for any non-zero initial state. Perform all your calculations manually (not using MATLAB).
(b) Now suppose u(t) = 1 for t ≥ 0. Describe what happens to the output signal for any non-zero initial state. Perform all your calculations manually (not using MATLAB).
2023-11-10