MAT 331 Fall 2023 Project Points of Increase
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MAT 331 Fall 2023 Project
Points of Increase
This project is based on the paper “Points of increase for Brownian motion” by Yuval Peres. A copy of this paper is available on the MAT 331 website. Consider a random walk on the integers that moves left or right at each step with equal probability. Let Xk denote the position of the random walk at step k (assume the walk starts at X0 = 0). Suppose the walk has N steps. We say n, for 1 ≤ n ≤ N is a point of increase if Xk ≤ Xn for all 0 ≤ k ≤ n and Xk ≥ Xn for all n ≥ k ≥ N.
(1) Write a MATLAB script that takes in a random walk (a list of real numbers) and checks whether this random walk has a point of increase or not. Test it on a random walk of length N = 1000 created by summing a sequence of random −1’s and +1’s.
(2) Choose a large M, say M = 10, 000, and repeat the experiment M times. How many times does the random walk have a point of increase?
(3) Peres’ paper gives an upper and lower bound for the probability that there is a point of increase in terms of quantities
pn = probability that Xk ≥ 0 for all 0 ≤ k ≤ n.
The precise values for these are given by
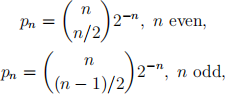
which you may use without proof (a proof is given in Section 6.11 of the book by Bishop and Peres, Fractals in probability and analysis which can be found on the homepage). Write code to compute these values. Note that p0 = 1, but that MATLAB arrays start with index 1, so you have to work around this somehow (there are several ways, e.g., make p a function instead of an array). For values of n up to around 1000, you can use the nchoosek command to compute the binomial coefficients, but you will get messages about lack of accuracy (these won’t effect your answer much). You can suppress warning messages in your output using the warning(’off’) command. Alternatively, using the formulas above, it is not hard to derive a formula for pn+2 in terms of pn, and using this will give a better result for much larger values of n.
(4) Using the formulas (3) and (5) in Peres’ paper, compute the lower and upper bound for the case you did in the experiment.
(5) How does your experimental result compare to the theoretical predictions?
2023-11-10