ACMA 355 Loss Models I - Assignment 3
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
ACMA 355 Loss Models I - Assignment 3
1. Twenty widgets are tested until they fail. The failure times are distributed as follows:

The exponential survival function S(t) = exp(−λ t) is used to model this process. Determine the maximum likelihood estimate of λ .
2. You are given the losses: 1000, 1200, 1600, 2100, 2200, 2400.
You fit an inverse exponential, with pdf

to the loss distribution using maximum likelihood.
Determine the resulting estimate of the probability of a loss below 1000.
3. The random variable X has survival function:
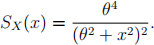
Two values of X are observed to be 2 and 4. One other value exceeds 4. Calculate the maximum likelihood estimate of θ .
4. Insurance covers 2 groups. Losses for the first group follow a two-parameter Pareto distribution with parameters θ = 1000 and α, and pdf
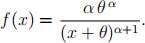
Losses for the second group follow a single-parameter Pareto distribution with the same two parameters, and pdf
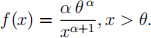
You observe the following losses for the first group: 700, 1000, 1500, and the following losses for the second group: 1200, 1700, 4000.
The parameter α is fitted using maximum likelihood. Determine α .
5. You are given:
(i) Loss payments for a group health policy follow an exponential distribution with unknown mean.
(ii) A sample of losses is: 100, 200, 400, 800, 1400, 3100.
Use the delta method to approximate the variance of the maximum likelihood estimator of S(1500).
6. Claim size X follows an inverse Pareto distribution with cdf
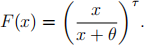
The two parameters τ and θ are estimated as 2 and 100, respectively; the covariance matrix of these estimators is

Estimate the variance of Pr(X > 500) when calculated using these estimators.
7. Size of loss has been fitted to a Pareto distribution using maximum likelihood. Esti-
mated parameters are α = 3, θ = 5000. The information matrix for (ˆ(α) , θ(ˆ)) is

Determine the upper bound of a 95% confidence interval for the mean of the Pareto distribution.
8. You are given:
(i) The distribution of the number of claims per policy during a one-year period for 10,000 insurance policies is:

(ii) You fit a binomial model with parameters m and q using the method of maximum likelihood.
Determine the maximum value of the loglikelihood function when m = 2.
9. You are given the following accident data from 100 insurance policies:
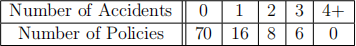
The data are fitted to a zero-modified negative binomial distribution with r = −0.5. Determine the fitted value of β .
10. The distribution of accidents for 84 randomly selected policies is as follows:
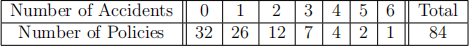
Which of the following models best represents these data (give the reasons)? (A) Negative Binomial (B) Discrete Uniform (C) Poisson (D) Binomial
2023-11-09