ST407 Monte Carlo Methods 2023–24 Assignment 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
ST407 Monte Carlo Methods 2023–24
Assignment 1
Transformation methods, rejection sampling, & importance sampling
Released: Thursday week 3, October 19th, 2023
Deadline: 13:00 on Thursday week 5, November 2nd, 2023
Recall the following:
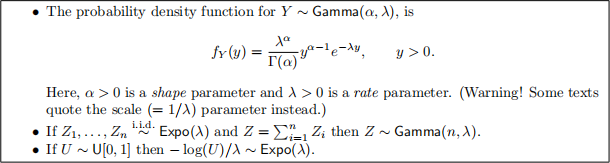
Hence, simulating from a Gamma(α, λ) distribution is straightforward when α is a positive integer.
1. Now let α > 1 be such that α 6∈ N. Consider using rejection sampling to produce samples from a Gamma(α, 1) distribution, with a Gamma(n, λ) proposal distribution and n ∈ N.
(a) What conditions on n and λ are necessary for rejection sampling to be possible?
(b) Let f(x) be the target density and g(x) the proposal density. Find
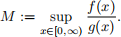
(c) Assume n = b αc , the largest integer less than α. Determine the optimal choice for λ.
2. Consider the bivariate density:
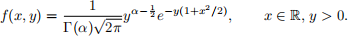
(a) Write an R function to evaluate this density for α = 2.5.
(b) Produce a plot to illustrate this density.
(c) Suppose Y ∼ Gamma (α, 1) and the joint density of ( X, Y ) is given by f(x, y). Find the condi-tional density of X | ( Y = y). Assuming samples from a normal distribution are available, use Q1(c) to suggest a proposal density g(x, y) for rejection sampling from f (x, y) when α = 2.5.
(d) Show that this algorithm has the same rejection constant M as in Q1. [You can also simplify M slightly here by noting that Γ(2.5) = 3 √ π/4 and Γ(2) = 1.]
(e) Implement this algorithm in R. Propose 1,000 samples and retain those which are accepted.
(f) Use your sample to estimate the mean vector and covariance matrix of (X, Y ). Compare your answer with the truth:
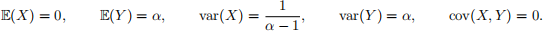
3. (a) Repeat Q2(e–f), this time using an importance sampling algorithm with the same proposal distribution as your rejection sampler.
(b) Perform a comparison between your rejection sampler and importance sampler. Use whatever sampling you feel is necessary in order to assess the relative performance of your two methods.
4. (a) Consider (X, Y ) drawn from f(x, y) as in Q2. For which of the following functions would you expect the antithetic variate (−X, Y ) to reduce the variance of an estimator of E[ϕ(X, Y )]?
Justify your answers.
(i) ϕ(x, y) = xy,
(ii) ϕ(x, y) = x 2y 2 ,
(iii) ϕ(x, y) = |x|y sin(x 3 ).
(b) Implement a Monte Carlo estimator in R to investigate whether antithetic variates improve the estimation of E[ϕ(X, Y )] when ϕ(x, y) = exp(x − (2y) −1 ).
5. (a) Use your knowledge of E(X | Y = y) and var(X | Y = y) from Q2(c) to obtain a Rao–Blackwellized estimator for E(X2Y 3/2 ).
(b) Implement a rejection sampler in R, again with α = 2.5, to obtain a realization of this estimator based on 1, 000 proposals. Compare its performance with a na¨ıve rejection method.
(c) What is the Rao–Blackwellized estimator for E(X √ Y + X2Y )? Comment on the implications for a Monte Carlo approach to this problem.
Some general guidance:
• You don’t need to write more than a few sides of text with some accompanying figures and code snippets to score very highly on this assignment. Your assignment should not exceed 15 pages in length and could be substantially shorter. Remember that it is responsible for just 10% of the module marks and use your time efficiently.
• If you write computer code in order to answer these questions then include that code as part of your answer. It would also be helpful, though not required, to attach to your assignment an R script file containing all your code.
• Apologies to anyone for whom this is obvious, but in Warwick assessment is taken very seriously and so the work you submit must be your own, it must be written in your own words and any computer code which is included as part of the solutions must be your own original work.
The following is a reproduction of the university’s written advice on cheating:
In the university regulations cheating is defined as an attempt to benefit oneself or another by deceit or fraud. The department recognises that discussing ideas about how to tackle questions is valuable part of the learning process. For assessments that are not explicitly group work you are required to work independently of other students. While collaboration in the sense of a discussion of general strategies or help of a general nature are allowed, detailed discussions and comparison of numerical results or computer code are not permitted. The work you submit should be written in your own words and you should not ask to see written work, computer code or computer output belonging to another student. If you hand work in claiming that it is your individual work and it is not this will be treated as cheating. Work produced by someone else may be included only provided it is appropriately acknowledged. Unacknowledged copying from either another student or from published sources including the internet is also treated as cheating.
For further details please consult the section on Academic Integrity in your course handbook.
2023-11-06
Transformation methods, rejection sampling, & importance sampling