MTH307: Problem set 3
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MTH307: Problem set 3
1. Let us do short-time discretization of the continuous time logistic equation, a.k.a Verhulst model:
 (1)
(1)
for r > 0 and K > 0.
(a) First, consider a fully explicit version:

Re-write this equation in the standard form Nt+τ = F(Nt). Find all the equilibria in this model. Find those values of τ for which the equilibrium at N = K is locally stable.
(b) Now, consider a semi-implicit version:
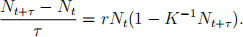
Again, re-write this equation in the standard form Nt+τ = F(Nt), find all the equilibria in this model, and investigate local stability of the equilibrium at N* = K.
2. Now let us do finite-time discretization of the same model,
 (2)
(2)
for r > 0 and K > 0.
(a) Recall, from lecture notes or previous homeworks, the formula for the solution N(t) of (2) with initial conditions N(0) = N0. Deduce from it the dependence of N(t + τ ) on N(t) for τ > 0. Show that the mapping N(t) → N(t + τ ) is described by a Hassell equation

and find the values of R, a and b in this equation in terms of the parameters r and K of the continuous-time model and the time interval τ .
(b) Compare thus obtained discrete-time model with the discrete time model ob-tained by short-time discretization in question 1 part 1b. Specifically, consider the case of small τ , such that τ → 0, t fixed, t/τ → ∞, using ex ≈ 1 + x for small x.
(c) Without further calculations, explain why this discrete-time model should have an equilibrium at N = K, and characterize its stability.
3. Now I would like to apply the Verhulst model to the algae population in my fish tank. Still, the dynamics of algae is different in the day and in the night, so I suppose that

where tm is the morning, te is the evening, t 0m is the next morning, te − tm = Td is the duration of the day and t 0m − te = Tn is the duration of the night, t 0m − tm = Td + Tn = 1 day.
(a) Using the results of part 2, obtain an expression for N(te) in terms of N(tm), rd, Kd and Td, and an expression for N(t 0m) in terms of N(te), rn, Kn and Tn. Combine these results to find the dependence Nn+1 on Nn, where Nn is the population size N(t) measured in the morning, t = tm of day number n, n ∈ Z. Show that this is a Hassel model Nn+1 = RNn/(1+aNn) b and determine parameters R, a and b in terms of parameters Rj , aj , j = d, n, found earlier.
(b) Determine the values of the parameters in the discrete-time model obtained in the previous part, for the following parameters of the original continuous-time model (3): Td = Tn = 0.5, rd = rn = 4 ln 2, Kd = 2, Kn = 1. Find the non-trivial equilibrium in this model and determine its stability (if the Hassell model has already been covered in the lectures, you can use the results obtained there).
(c) Sketch the solution of equations (3), corresponding to the nontrivial equilibrium found in the previous part, during two consecutive days, i.e. for t ∈ [0, 2]. Find the maximal and minimal densities of the algae population.
2023-11-02