Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

PHS2062

Electromagnetism and Optics – Paper 1 of 1

Section A: Electromagnetism

Please use separate script books for Section A and Section B of this examination.

Question 1: Electrostatics (20 marks)

(a) (4 marks) “Gauss’s law is always true, but it is not always useful” (D.J. Grif- fiths). Explain what is meant by this statement, and particularly the circum-stances under which Gauss’s law for electrostatics can be used to determine the electric field strength. It would suffice for your answer to be in terms of general principles – particular examples are not necessary.

Consider a conducting spherical shell with inner radius a and outer radius b that carries net charge Q. Suppose that there are no charges within the central cavity.

(b) (1 mark) What is the electric field strength within the conducting spherical shell?

Figure 1: Cross-section through a conducting spherical shell, with inner radius a and outer radius b. There are no charges inside the cavity, but the conductor itself carries net charge Q.

(c) (5 marks) Use the symmetry of the present problem together with Gauss’s law to argue that the net charge Q on the conductor must be uniformly distributed over the conductor’s outer surface.

Hint: apply Gauss’s law to a spherical surface with radius ever-so-slightly smaller than b, bearing in mind your answer to part (b).

It can be shown (but you are not being asked to do so) that the electric field is given by

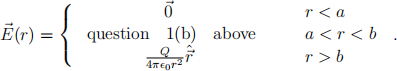            (1)

(d) (5 marks) Setting the zero reference of potential to be at spatial infinity, cal-culate the potential V (~0) at the centre of the cavity inside the conductor by suitable use of the identity

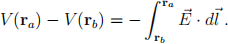                   (2)

Note: If you can guess the answer to this it will be a good check on your result, but for full credit you must derive the result using the approach specified.

Figure 2: Cross-section through conducting spherical shell, with inner radius a and outer radius b. There is now a point particle with charge q at the centre of the cavity. The conductor itself still carries net charge Q.

(e) (1 mark) Suppose we bring a point particle with charge q from spatial infinity in to the centre of the cavity, producing the configuration shown in Fig. 2. Assume the charge q is so small in comparison to the charge Q on the conductor that the charge distribution on the conductor is unaffected by the passage of the point particle. What work was required to bring the point particle in from spatial infinity to its location at the centre of the cavity? Express your answer in terms of V (~0) defined in part (d).

Note: If you are fretting about how the particle got through the spherical shell, assume a tiny hole opened up in the shell to let the point particle inside and then closed again, and that this process involved no work.

Now suppose that the point charge remains within the centre of the spherical cavity, but that the spherical cavity is shifted off-centre within the conducting shell as shown in Fig. 3. (How this could be achieved is irrelevant to the present problem.)

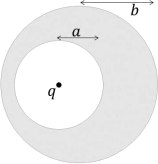
Figure 3: Cross-section through conducting shell, with outer radius b and containing a spherical-but-off-centred cavity of radius a. There is a point particle with charge q at the centre of the cavity. The conductor itself still carries net charge Q.

(f) (4 marks) Explain why, despite the spherical symmetry of the overall configu-ration having been broken in Fig. 3, the electric field within the cavity is still a Coulomb field ~E(r) = 4π/q0r 2 ~rˆ, with origin taken to be at the location of the point charge at the centre of the cavity.

Note/hint: Partial credit would be awarded for insightful motivations on physical grounds, but a rigorous answer to this question requires using the uniqueness property of the solution of Poisson’s equation.

Question 2: Potential theory and electrostatic analogues   (13 marks)

(a) (6 marks) Drawing from areas of physics other than electromagnetism, and sim-ilarly excluding the specific examples appearing later in this question, give two example of scalar fields and two examples of vector fields. Briefly justify why your examples are indeed fields of the kind indicated.

Fick’s law for diffusion for neutrons states that the “diffusion flux vector” J~, i.e. the number of neutrons crossing a surface per unit area per unit time, is proportional to the gradient of the number density of neutrons (i.e. the number of neutrons per unit volume) N(x, y, z):

J~ = −D∇N ,           (3)

where D is the diffusion constant. In the time independent case, it can also be shown that

∇ · J~ = S ,              (4)

where S(x, y, z) is a source/sink term describing the number of neutrons gener-ated/absorbed per unit volume per unit time.

(b) (3 marks) Suppose we have a compact, spherically-symmetric region which is a source of neutrons. Starting from Eq. (4), argue that outside this source region the diffusion flux of neutrons drops off according to an inverse-square law (i.e. as 1/r2 ).

Note: You do not need to provide rigorous derivations “from first principles”. Rather, it would suffice to explain the mathematical equivalence with electro-statics and reason via analogy to that case.

(c) (2 marks) Assuming that D is a constant (rather than a field), demonstrate that N(x, y, z) satisfies Poisson’s equation.

(d) (2 marks) In a region containing no sources/sinks, N(x, y, z) satisfies Laplace’s equation. Argue that within such a region the number density of neutrons N(x, y, z) can have no local minima.

Note: Again, you do not need to provide rigorous derivations “from first prin-ciples” – it would suffice to explain the mathematical equivalence with electro-statics and reason via analogy to that case.

Question 3: Magnetostatics and electrodynamics       (27 marks)

(a) (3 marks) Reduce (the relevant) Maxwell’s equations to give the two equations for magnetostatics (either integral or differential form is fine). Please state any assumptions made.

Consider a straight, infinitely-long coaxial cable consisting of a solid, central wire core of radius a surrounded by a very thin (i.e. such that its thickness is negligible) outer wire sheath with radius b. Suppose that the wire core carries current I traveling to the right and uniformly distributed across its cross-section, while the outer sheath carries current I traveling to the left and uniformly distributed across its circumference. For the purposes of this problem, suppose the space between the central wire core and the outer sheath is empty (treating it as if in vacuum). This configuration is shown in Fig. 4.

Figure 4: Portion of the coaxial cable consisting of a solid, central wire core of radius a (which carries a current I towards the right) surrounded by an outer wire sheath of radius b (which carries a current I towards the left). Treat the space between central wire core and outer wire sheath as if in vacuum.

Adopt a cylindrical coordinate system (s, φ, z) with z-axis coincident with the central axis of the cable.

(b) (2 marks) Write down the expression for the current density J~ (the current-per-unit-area, with vector direction) within the central wire core.

(c) (8 marks) Using Ampere’s law, carefully demonstrate that the magnetic field is given by

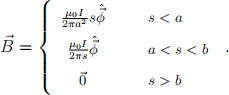              (5)

In this context “carefully” means that for full credit you need to justify your choice of Amperian loop, the value deduced for R~B · d~l for that loop and, within all three regions (i.e. for s < a, for a < s < b and for s > b), the current passing through the loop.

Note: You can assume – without providing any justification for it yourself – that any magnetic field will be azimuthally directed (i.e. in the ~ ˆφ direction) and depend on neither φ nor z.

In magnetostatics, for any particular magnetic field distribution ~B it is possible to find/construct a magnetic vector potential ~A such that

~ B = ∇ × ~A . (6)

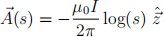           (7)

is a suitable vector potential for the magnetic field in Eq. (5) for a < s < b, i.e. inside the space between central wire core and outer wire sheath.

(e) (2 marks) Further, show that ∇ · ~A = 0 for ~A as given in Eq. (7).

Suppose instead that the current within this coaxial cable is an alternating current:

I(t) = I0 sin(ωt) . (8)

Further suppose that the current is sufficiently slowly varying that the magnetostatic solution of Eq. (5) still holds for the now time-varying magnetic field:

         (9)

(f) (4 marks) Using Faraday’s law, derive an expression for the electromotive force induced in a small rectangular wire loop introduced into the a < s < b region with dimensions as shown in Fig. 5.

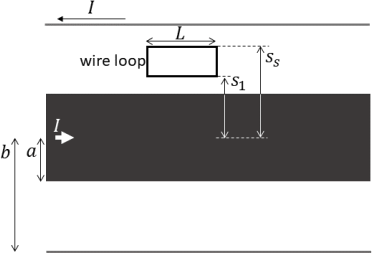
Figure 5: Cross-section through coaxial cable with wire loop sitting in the s-z plane (extending in the radial direction from s1 to s2 and with length L along the z-axis) between the central core and the surrounding sheath.

(g) (4 marks) Argue that the electric field induced by this time-changing magnetic field will be axially directed (i.e. along the ~zˆ direction).

Hint: identify similarities in the equations satisfied by ~E and ~A.