Remark:

. Please submit both your R script and log file.

. Write a comment for each step to explain your following codes.

. Implement the programming style to your codes from thisblog

This assignment uses Newton’s method to calculate the implied interest rate deter-

mined by a price for an annuity.

Suppose we have a function f (x) and that we have code to evaluate f (x) and f ′ (x)  for any x. We have a number a and we want to find x∗ so that f (x∗) = a.  This is  sometimes called “root finding”,because x∗ is a “root” of the equation f (x)−a = 0.  The term “root” originally applied to polynomials, but now is used for the “zeros”

( x values where f (x) = a = 0 ) of any function.

Newton’s method constructs a sequence of iterates xn for n = 1, 2, . . ., that we hope

have the property that

xn → x∗ as n → ∞

You stop the code when you think xn is close enough to x∗ .  Newton’s method is iterative, it involves a sequence of iterations.  That means, it does the same thing (with different numbers) over and over. It is derived by imagining that xn is close to x∗ .

We approximate f (x∗) by Taylor expansion up to the first derivative term around xn. That is

f (x∗) = f (xn + (x∗ − xn)) ≈ f (xn) + f ′ (xn) (x∗ − xn) .

We approximate the equation f (x∗) = a with the approximation

f (xn) + f ′ (xn) (x∗ − xn) ≈ a

We choose the next iterate xn+1  by changing this approximation into an equation

f (xn) + f ′ (xn) (xn+1 − xn) = a.

At iteration n, we know xn. We write code to evaluate f (xn) and f ′ (xn). Then we can solve for xn+1. The algebra leads to

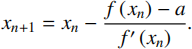            (1)

The core of Newton’s method is to apply the formula (1) over and over until you

think xn is close enough to x∗ , or until you decide it is not working.

The first “iterate”, which we call x1  (it sometimes is called x0  ) is the initial guess. The programmer has to find some guess at the solution. This isn’t fun. It often in- volves drawing graphs and playing with simple approximations. This is ”problem specific”, which means it depends on the specific formula for f (x) and the shape of the graph and the value of a. The iteration formula (1) is not problem specific.

But if you have a poor initial guess, the method is more likely to fail.

It is a theorem that iff ′ (x∗) * 0 and if x1  is close enough to x∗ , then xn → x∗ as n → ∞. Moreover, xn converges fast. xn+1  is much closer to x∗ than xn is.  But if the initial guess is poor, then xn may not converge to x∗ .  On the contrary, it may happen that xn → ∞ as n → ∞. This is common. It is important to spend the time to find a good initial guess.

But despite your best efforts, your Newton’s method code will sometimes fail to converge.  You need something in your code to make sure the iteration (1) is not an infinite loop.  You can do this by defining a parameter nmax  and stopping the program if n > nmax . If this happens, the program should return an error message saying it didn’t work.  In practice nmax   = 20 is probably fine, but nmax   = 100 also

is OK.

You also need a convergence criterion, a condition that tells you when to stop and declare victory. You can define a small number E and declare convergence if |xn+1 − xn | ≤ E. If you want an interest rate to within one basis point, and ifr has units of interest per year, then you can take E = 10−4. But this isn’t so small. If the code can get to 10−4  it probably get to 10−10. Try a small E until you learn it’s too small.

Apply your code to calculating the interest rate r implied by the price of an annuity. If r is an interest rate, C is the annual payment rate, mis the number of payments per year, and T is the number of years, then the present value is

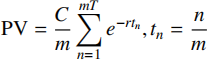           (2)