Homework 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Homework 2 (out of 100 points)
Problem 1 (Performance of a Flexibility Network) [20 points]
Consider a system with m resources and n demand types, with resource i has capacity ci . A (bipartite) flexibility network is defined by its biadjacency matrix F, which is a m by n binary matrix, where Fij = 1 indicates that resource i is connected to demand type j (i.e., resource i can be used for demand type j). Given a demand instance vector d in R n +, the total demand satisfied by network F, denoted as P(d, F), is the objective value of the following LP:
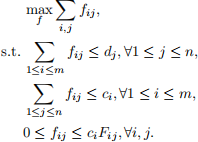
The performance of a flexibility network F is the expected total demand satisfied by F under random demand vector D, defined as ED[P(D, F)]. For the question, we will assume that m = n = 10, ci = 1000 for all i, and D1, . . . , Dn are i.i.d. random variables uniformly distributed from 500 to 1500. Also, we will estimate the performance of different networks F via Monte Carlo simulation. That is, we will randomly draw demand instances d 1 , d 2 , ..., d 1000 from the given distribution of D. Then, for the three different networks described below, we will estimate its performance by
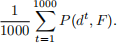
a) Based on the Monte Carlo procedure described above, estimate (using any open-source or commericial linear programming solvers):
i The performance of flexiblity network defined by F, where F is the identity matrix. Note that the network is simply 10 disjoint edges, and it is known as the dedicated network.
ii The performance of flexiblity network defined by F, where Fij = 1 whenever i = j, j ≡ i + 1 mod n, and Fij = 0 otherwise. Note that the network is a cycle connecting all the nodes in the bipartite network.
iii the performance of flexiblity network defined by F, where F is the matrix of all ones. Note that the network is known as the fully flexible network.
b) Show that for a fixed demand instance d, P(d, F) can be formulated as a max-flow problem.
Problem 2 (Fractional Programming) [20 points] Consider the following linear fractional optimization problem:
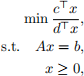 (LFP)
(LFP)
where A ∈ R m×n. Now consider
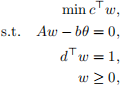 (RLP)
(RLP)
a Show that the objective function of LFP, in general, is not convex.
b Show that if RLP has an optimal solution, then both RLP and LFP have the same optimal objective function values.
c Show that for every basic feasible solution of LFP there is a corrresponding basic feasible solution of RLP.
d Suppose that the feasible region of LFP is bounded. Show that for every basic feasible solution of RLP there is a corresponding basic feasible solution of LFP.
Problem 3 [20 points] Prove or give a counterexample to the following statement: If the optimal solution to the primal is unique, then there is an optimal solution to the dual that is nondegenerate.
Problem 4 [20 points] Given matrix A1 ∈ R m1×n, A2 ∈ R m2×n, and vectors b1 ∈ R m1 , b2 ∈ R m2 . Prove that exactly one of the following holds:
• There exists x ≥ 0 that satisfies: A1x < b1 and A2x ≤ b2
• There exists (y1, y2) ≥ 0: that satisfies: A>1 y1 + A>2 y2 ≥ 0, and either (i) b >1 y1 + b >2 y2 < 0; or (ii) b >1 y1 + b >2 y2 = 0 and y1 = 0.
Problem 5 (Strong Complementary Slackness) [20 points] Given linear program
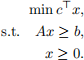 (P)
(P)
Prove that there exists an optimal solution x ∗ to (P) and an optimal solution y ∗ to the dual of (P) such that

where Aj is the j-th column of A and aTi is the i-th row of A. Hint: Use the previous problem.
Problem 6 (Lipschitz Continuity w.r. to LP RHS) [20 points] Define F(b) as the optimal value of the linear program
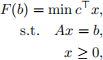
for any b ∈ S := {Ax | x ≥ 0}. Suppose that {y | A> y ≤ c} is nonempty. Prove that there exists some constant C (which may depend on A ∈ R m×n and c ∈ R n) such that for any b, b 0 in S, we have
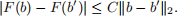
Hint: You may need Cauchy–Schwarz inequality, that is, |x > y| ≤ kxk 2 · kyk 2, for any vectors x and y.
Problem 7 [20 points] Consider the problem
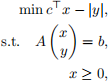
where x ∈ R n, y ∈ R, A ∈ R m×(n+1). Transform this problem into a linear optimization model.
Problem 8 (optimization with logistic model) [20 points] A random variable X ∈ {0, 1} satisfies
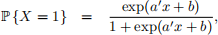
where x ∈ R n is a vector of variables that affect the probability, and a ∈ R n and b ∈ R are known parameters. We can think of X = 1 as the event that a consumer buys a product, and x as a vector of variables, such as advertising efforts or prices, that affect this probability. x is subject to a set of linear constraints, i.e., x must satisfy F x ≤ g for some matrix F ∈ R m×n and vector g ∈ R m. Formulate the following problems as convex optimization problems.
(a) The problem of maximizing P {X = 1} over all feasible x.
(b) Let c 0 x + d be the profit derived from selling the product, assumed positive for all feasible x, for some known parameters c ∈ R n, d ∈ R. The problem of interest is maximizing the expected profit, i.e., P {X = 1} (c 0 x + d), over all feasible x.
2023-10-24