Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

IEOR-4307

Problem Set #2

Fall 2023

Due: BEFORE CLASS September 28, 2023

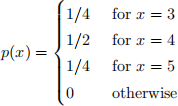
We will collect a sample of size n = 800 from this distribution:  X1, X2 ,..., X800 , and we will use it

to compute the sample mean X(¯). Answer the following questions:

(a) What is the limiting distribution (as ngoes to infinity) of X(¯)? Also provide mean and variance.

(b) We are interested in the probability that the value of the sample mean will be less or equal

than 81/20, that is P(X(¯) ≤ 81/20).  Using the limiting distribution from the previous point,

find that probability. You can use your favorite software to compute the value of the CDF.

Ex. 2 (1 pt).

We are interested in studying defects in a manufacturing process for a medical device. Let p be the probability that a device is defective. Do the following

(a)  Define a random variable X that encodes whether the next device is defective or not.  What is the probability mass function of X?

(b) We plan to collect a sample X1,..., Xn. What is an unbiased estimator ˆ(p) for p?  Prove that it is unbiased.

(c) What is the limiting distribution of your estimator (including mean and variance)?

(d) Now fix p = 0.05 = 5% and n = 100.  What is the probability that your estimator ˆ(p) will take

a value greater than 0.06? You can use your favorite software to compute this probability.

Ex. 3 (2 pt).

Suppose that X1,..., Xn  are independent and identically distributed Poisson random variables with parameter λ. The probability mass function of a Poisson random variable is

and for a Poisson variable we also know that E[Xi] = λ and V(Xi) = λ.  Do the following:

(a)  Derive the maximum likelihood estimator (MLE) of λ

(b) What is the asymptotic distribution of the MLE (including its mean and variance)?

(c)  Suppose that, instead of the random variables defined above, we only observe the events

Xi = 0                      or             Xi  > 0,

for i = 1,...,n.  Derive the MLE of λ under this new setting. Hint: define a new discrete random variable Yi  that takes value 0 when Xi  = 0 and value  1 when Xi  > 0.  What is the distribution of the random variable Yi  as a function of λ?  Use the observations Y1,...,Yn  to find the new MLE of λ .

Ex. 4 (1 pt).

Let X1,..., Xn  ∼ N(µ,1). Let τ = eμ .

(a) What is ˆ(τ), the maximum likelihood estimator for τ?

(b)  Use the Delta method to get the standard error sˆe ofˆ(τ) .

(c)  Using your favorite software and assuming µ = 5, n = 200, generate a random sample of size n and compute the values of the quantities derived in parts (a) and (b).  Hint: in R, the function rnorm(n,µ,σ) can be used to generate a sample of size n. In Python: random.normal(loc=µ, scale=σ, size=n) from the library numpy. In Sheets, you can generate a single random value from the normal distribution with NORMINV(rand(), µ, σ), like in the example from Lecture 1.  Please either report your code in your pdf submission, or a screenshot of it  (it won’t be graded, but it might be used as a reference to understand the reported results).