Math 453. Proof portfolio 2.
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Math 453. Proof portfolio 2.
2 Odd perfect numbers
Note: You will encounter some numerical computations (e.g. (1 + 1/3 + 3 12 )(1 + 1/11 + 1 11 2 ) < 2).
You can compute such things with a computer and assert them without giving details.
The big goal is to prove the following:
Theorem 2.1. If n is an odd perfect number then n has at least 4 distinct prime factors.
We will accomplish this by proving a sequence of lemmas. We have already seen that a number with only one prime factor cannot be perfect. We recall the formulas
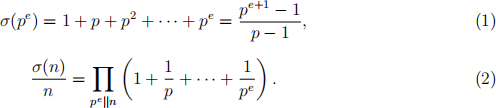
You can reference these by using (1), (2).
We prove a Lemma to get started.
Lemma 2.2. If n = p e11 · · · p e t t is an odd perfect number, then exactly one of the exponents ei is odd. For this i we have pi +1 2 | n.
Proof. We have σ(p e ) = 1 + · · · + p e ≡ e + 1 (mod 2). Since σ(n) = 2n and n is odd, exactly one of the factors σ(p e i i ) is even. So exactly one of the ei is odd.
Since ei is odd, (1 + pi) | (1 + pi + p 2 i + · · · + p e i i ). So (1 + pi) | σ(p e i i ). Since σ(n) = 2n, we see that (1 + pi) | 2n. The result follows.
Your job is to fill in the rest of the proofs below.
Lemma 2.3. For any n we have
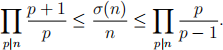
Proof. Note that when n = 1 the result is true, so we may assume in the proof that n ≥ 2.
Corollary 2.4. There are no odd perfect numbers with exactly two distinct prime factors.
Proof.
Lemma 2.5. If n = p a q b r c is an odd perfect number with exactly three prime factors p < q < r, then
n = 3a 5 b 7 c , or n = 3a 5 b 11c , or n = 3a 5 b 13c , where b is odd, and a, c are even.
Proof. Hint: First rule out all other possibilities for the three primes.
Lemma 2.6. If n is an odd perfect number with exactly three prime factors then
n = 3a 5 b 11c , where b is odd and a, c are even.
Proof. Hint: If e is even and p ≡ 2, 3 (mod 5), what can you say about σ(p e ) (mod 5)?
Lemma 2.7. If n is an odd perfect number with exactly three prime factors then
n = 3a 5 b 11c , where b ≥ 3 is odd, a = 2, and c is even.
Proof. Hint: First rule out b = 1 by working modulo a small power of 2. Then rule out a ≥ 4.
We can now finish the proof.
Proof of Theorem 2.1.
2023-10-18