闪电代写 -代写CS作业_CS代写_Finance代写_Economic代写_Statistics代写_代码代做_IT代写_加急帮助

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Physics 101

Practice Final

FINAL EXAM

(1). (15 points total) The exponential integral of order n is defined to be:

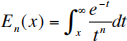
(a). (5 points) Use integration by parts to show that:

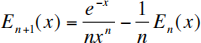
(b). (5 points) Find the leading order asymptotic behavior of En (x) as x → ∞ .

(c). (5 points) Show that the remainder (the difference between En (x) and the leading term in part (b)) is higher order, i.e. the absolute value of the remainder is strictly smaller than the leading term by a factor that goes to zero as x → ∞ .

(2). (30 points total) This problem involves using the map w = log(<) to find the steady state temperature T and the heat flux Ψ in a circular sector of angle θ = π /4 in the z − plane. T and Ψ both satisfy Laplace’s Equation and are harmonic conjugates. The problem is continued on the next page.

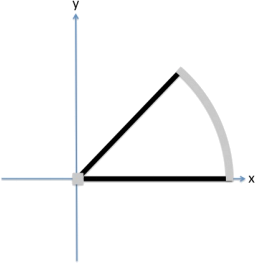
(a). (10 points) The boundaries of the region in the z −plane ( z = x + iy) are shown below. T = 0 on the real axis for 0 < x < 1. T = 1 on upper boundary of the sector, i.e. on the line segment z = reiπ /4 with 0 < r < 1. There is a small insulating strip at the origin. The circular arc from z = 1 to z = eiπ /4 is also insulating. The region of interest is the circular sector inside of these boundaries.

Use the map w = log(<) to identify the corresponding ” −plane boundaries ( w = u+ iv). The letters A, B, C label points z = 1, z = 0 , and z = eiπ /4 in the z −plane. Identify (in the table) and label (on the axes given) the corresponding points in the ” −plane. Label the T = 0 , T = 1, and all insulating boundaries in the ” −plane. Choose a point D in the interior region in the z −plane and identify the corresponding point in the ” −plane to show which region of the ” −plane correspond to the interior of the sector. To receive full credit on this part you must complete both the table and the figure.

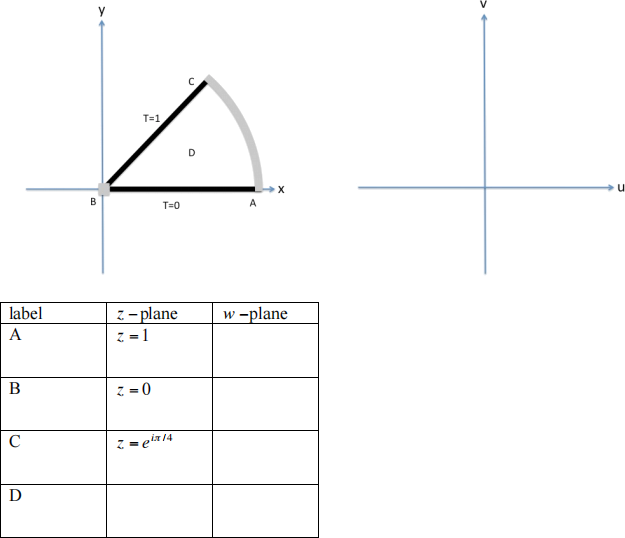
(b). (10 points) Write down the solutions of Laplace’s equation for the steady state temperature T(u,v) and the heat flux Ψ(u,v) in the ” −plane in the region that corresponds to the circular sector in the z −plane. Include a sketch using solid lines to illustrate the constant temperature curves T(u,v) = constant, and dashed lines to illustrate heat flux lines Ψ(u,v) = constant in the ” −plane. Include the boundaries from part (a) in your sketch.

(c). (10 points) Use the map w = log(<) to solve for the steady state temperature T(x , y) and the heat flux Ψ(x , y) in the z −plane. Include a sketch using solid lines to illustrate the constant temperature curves T(x , y) = constant and dashed lines to illustrate heat flux lines Ψ(x , y) =constant in the circular sector in the z −plane.

(3). (30 points total) This problem involves solving the following differential equation for t = 0 using the Laplace Transform method:

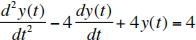
with y(0) = 0 and y' (0) = (dy /dt)t =0 = −2 . You must use Laplace Transforms to receive credit for this problem. You must use contour integration to invert the transform. The problem is continued on the next page.

(a). (5 points) Compute the Laplace Transform of the function f (t) = 4 .

(b). (10 points) Laplace Transform the second order differential equation above (i.e. let Y(s) = y(t)e − stdt and write the corresponding equation which is satisfied by Y(s)). You will need to include the Laplace Transform of f (t) = 4 from part (a). Solve the equation to obtain the solution for Y(s) in the transformed s − space.

(c). (15 points) Invert the transform using the Bromwich Integral (i.e. Inverse Laplace Transform) y(t) = Y(s)e stds to obtain the solutions for y(t) satisfying the original equation for t = 0 . You must use the Bromwich Integral and evaluate the integral using contour integration to receive credit for this part. Justify your integration steps.

(4). (30 points total) This problem involves finding the Green’s Function for the following differential equation for y(x) :

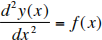
where 0 = x = 1, y' (0) = dy /dx x =0 = 0 , and y(1) = 0 , and then solving for y(x) for a specific f (x) using the Green’s Function. This problem is continued on the next page.

(a). (5 points) Write down the corresponding differential equation and boundary conditions for the Green’s Function G(x , x ') .

(b). (15 points) Solve for G(x , x ') using the explicit method. The explicit method (developed in class and Boas) involves using the two linearly independent solutions to the homogeneous equation, which in this case are u1 (x) = 1 and u2 (x) = x , applying the boundary conditions, and then matching solutions for the homogeneous equation at x = x', where the Green’s Function is continuous, and the first derivative has a discontinuity equal to unity, i.e., Δ [dG(x , x ')/dx]x =x ' = 1.

(c). (10 points) Using the Green’s Function method, find the solution y(x) that satisfies the original equation when f (x) = x for 0 = x = 1. You must use the Green’s Function to receive credit on this part.

(5). (30 points total+5 points extra credit) This problem involves solving a differential equation for y(x) using Fourier Transforms. The equation is:

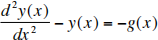
A specific function g(x) will be given in part (b). The functions y(x) and g(x) go to zero as x → ±∞ and their Fourier Transforms exist. This problem is continued on the next page.

(a). (5 points) Defining Y(k) = y(x)exp(−ikx)dx and G(k) = g(x)exp(−ikx)dx , Fourier Transform the differential equation given above, and solve for Y(k) in terms of this general G(k) .

(b). (5 points) Compute the Fourier Transform G(k) for the specific function:

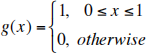
In part (c) on the next page you will substitute this into your solution for Y(k) from part (a) and invert the transform.

(c). (20 points+5 points extra credit) Substitute your result for G(k) from part (b) into your general solution for Y(k) from part (a). Then invert the Fourier Transform using contour integration to find the solution y(x) = Y(k)e ikx dk that satisfies the differential equation:

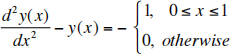
(This is just the equation you get when you put the g(x) from part (b) into the equation part (a).) Justify the steps of your contour integration.

The required (20 points) part of the problem is to obtain the solution y(x) for 0 = x = 1. For extra credit (additional 5 points), obtain the complete solution y(x) for −∞ < x < ∞ .