COMP2022/2922 Automata S2 2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COMP2022/2922 Automata
S2 2023
After this tutorial you should be able to:
1. Express in English the language of a DFA/NFA.
2. Design DFAs/NFAs for languages specified in English.
3. Convert RE to NFAs
4. Form a DFA for the union or intersection of two DFAs using the product construction.
5. Devise algorithms for solving certain decision problems about DFAs/NFAs
1 DFA
Problem 1. For each of the following DFAs:
(a) Give (Q, Σ, δ, q0, F) for the automaton.
(b) Give a precise and concise English description of the language recognised by this automaton.

Problem 2. Draw the following automaton and give the language that it recog- nises:
• Q = {q1, q2, q3} is the set of states.
• Σ = {b, c, d} is the alphabet,
• q1 is the start state.
• F = {q2} is the set of accept states,
and the δ : Q × Σ → Q is given by the following table:
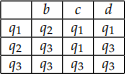
Problem 3. Prove that the following languages are regular, by drawing DFAs which recognise them. The alphabet for all the languages is {a, b, c}.
1. Strings that start with b
2. Strings that end with b
3. Strings that contain exactly one b
4. Strings that contain at least one band are of length exactly 2
Problem 4.
1. Construct a DFA which accepts strings of 0s and 1s, where the number of 1s modulo 3 equals the number of 0s modulo 3.
2. Construct a DFA which accepts binary numbers that are multiples of 3, scanning the most significant bit (i.e. leftmost) first. Hint: let each state ’remember’ the remainder of the string read so far.
3. Using the previous automaton, construct an automaton which accepts bi- nary numbers which are NOT multiples of 3.
2 NFA
Problem 5. Consider the following NFA:
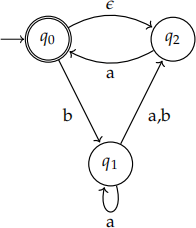
Does the NFA accept:
1. ϵ
2. a
3. baba
4. aaab
Problem 6. Draw an NFA for each of the following languages. The alphabet is Σ = {a, b, c}. You may use epsilon transitions.
1. Strings that end with aa (use only 3 states)
2. Strings that contain the substring ‘bbc’ (use only 4 states)
3. Strings that start with a or end in c (use only 4 states)
4. Strings that start with a and end in c (use only 3 states)
3 From RE to NFA
Problem 7. Use the construction demonstrated in lectures to construct an NFA for each of the following REs:
1. 0* 110*
2. ((00)* (11) |10)*
4 Algorithms
Problem 8. In this problem you will show that the regular languages are closed under union. That is, if M1, M2 are DFAs, then so is L(M1) a L(M2) = L(M) for some DFA M.
Hint. Simulate both automata at the same time using pairs of states.
1. Argue why the construction is correct.
2. Use the construction to draw a DFA for the language of strings over alpha- bet {a, b} consisting of an even number of a’s or an odd number of b’s.
Problem 9. The non-emptiness problem for DFAs is the following decision problem: given a DFA M, return ”Yes” if L(M) ![]() ∅ and ”No” otherwise.
∅ and ”No” otherwise.
Devise an algorithm for solving this problem. What is the worst-case time com- plexity of your algorithm?
How would you adapt your algorithm to solve the non-emptiness problem for NFAs?
Problem 10. The equivalence problem for DFAs is the following decision problem: given DFAs M1, M2, return ”Yes” if L(M1) = L(M2), and ”No” otherwise.
Devise an algorithm for solving this problem. What is the worst-case time com- plexity of your algorithm? What about space complexity (i.e., amount of mem- ory needed)?
Hint. Use the facts that the regular languages are closed under the Boolean operations (i.e., complement, union, intersection), and the fact that the emptiness problem for DFAs is decidable.
Problem 11. (Exam 2022) Fix Σ = {0, 1}. Consider the operation delzero that maps a string u to the string in which every 0 is deleted. So, e.g., delzero(0) = ϵ, delzero(01101) = 111, delzero(1) = 1, and delzero(ϵ) = ϵ. For a language L 己 Σ*, let delzero(L) = {delzero(u) : u e L}. Explain why if L is regular, thendelzero(L) is regular.
Problem 12. (Hard) A fundamental problem in string processing is to tell how close two strings are to each other. A simple measure of closeness is their Ham- ming distance, i.e., the number of position in which the strings differ, written H(u, v). For instance, H(aaba, abbb) = 2 since the strings disagree in positions 2 and 4 (starting the count at 1). Positions at which the the strings differ are called errors.
Let Σ = {a, b}. Show that if A 己 Σ* is a regular language, then the set of strings of Hamming distance at most 2 from some string in A, i.e., the set of strings u e Σ* for which there is some v e A such that len(u) = len(v) and H(u, v) 三 2, is also regular.
Hint. Take a DFA M for A, say with state set Q, and build an NFA with state set Q × {0, 1, 2}. The second component tells you how many errors you have seen so far. Use nondeterminism to guess the string u ∈ A that the input string is similar to, as well as where the errors are.
How would you change the construction to handle Hamming distance 3 instead of 2?
How would you change the construction to handle that case that we don’t re- quire len(u) = len(v)? e.g., H(abba, aba) = 2.
p.s. The problem of telling how similar two strings are comes up in a variety of settings, including computational biology (how close are two DNA sequences), spelling correction (what are candidate correct spellings of a given misspelled word), machine translation, information extraction, and speech recognition. Of- ten one has other distance measures, e.g., instead of just substituting characters, one might also allow insertions and deletions, and have different ”costs” asso- ciated with each operation. The standard way of computing similarity between two given strings is by Dynamic Programming, an algorithmic technique you will delve into in COMP3027:Algorithm Design.
2023-09-04