Problem 1

Gomoku is a two-player game played on a 15×15 board. On player 1’s turn, they place a white stone on one square on the board; player 2 does the same with a black stone on their turn.  The same square may not be occupied twice, and the first player to align five stones in a row horizontally, vertically, or diagonally wins. Assuming player 2 always moves second, show that player 2 cannot have a winning strategy.

Solution. We use a strategy-stealing argument. Assume for the sake of contradiction that player 2 has a winning strategy S. Play a game of gomoku as follows:

•  On their first turn, player 1 places a stone arbitrarily.

• Player 2 plays S.

• From their second turn on, player 1 uses strategy S with the white stones. If S requires that player 1 move on an occupied square, move arbitrarily.

Then player 1 is using S from a starting position where there is one additional white stone on the board. Since an extra white stone cannot hurt player 1, strategy S is also winning for the second player starting from this position with an extra stone, so player 1 wins this game.  Thus player 1 and player 2 both win, which is impossible.  We conclude that player 2 cannot have a winning strategy.

Problem 2

(a)  Consider the game Nim.  Determine if (3, 2, 1) is a P or N-position.  Also check the position (4, 2, 1).

(b)  Consider a variant of Nim in which players have an additional move option: on a player’s turn, they may combine two piles into one. Give an example of a P-position in Nim which becomes an N-position in this variant.

(c)  Give an example of an N-position in Nim which becomes a P-position in this variant.

Solution.  (a)  Use Nim sums. In binary we have 3 = 11, 2 = 10, and 1 = 01. Their Nim sum is 0, so (3, 2, 1) is a P-position. We also have 4 = 100 in binary, so the Nim sum for (4, 2, 1) is 111  0. Therefore (4, 2, 1) is an N-position.

(b) We claim (3, 2, 1) is a P-position in Nim which becomes an N-position with the extra move allowed. To show this, we need to prove that the next player can make a move from position (3, 2, 1) to a position that is a P-position (we know by part (a) that it is a P-position in Nim). Suppose player 1 (who we will assume moves next throughout this problem) merges the second two piles, giving player 2 the position (3, 3). This new position is a P-position in regular Nim, and we will be done if we can show it is a P-position in the variant, too. To see that this is the case, note that, assuming best play, neither player will choose to merge piles when there are only 2 piles left, as this allows the opponent an immediate win. So the P and N-positions with at most 2 piles agree for Nim and this variant.  We conclude that (3, 3) is a P-position in the variant,since its Nim sum is zero. Thus (3, 2, 1) is an N-position in the variant, as claimed.

(c) We claim (4, 2, 1) is an N-position in Nim which becomes a P-position with the extra move allowed. To show this, we need to prove that every move that the next player can make from (4, 2, 1) lands on an N-position (we know by part (a) that it is an N-position in Nim).

•  If player 1 makes a merge, the possible resulting positions are (5, 2), (4, 3), and (6, 1). These are all two-pile positions with nonzero Nim sums, so they are N-positions in the variant.

•  If player 1 removes all coins from one pile, the resulting positions are (2, 1), (4, 1), and (4, 2).  Again, these are all two-pile positions with nonzero Nim sums, so they are also N-positions in the variant.

•  It remains to analyze moves where player 1 removes some, but not all, coins from one pile.  We do these individually.  If player  1 removes one coin from the second pile, the result is (4, 1, 1), which is an N-position as player 2 can respond by taking all coins from the first pile, leaving player 1 with the P-position (1, 1).

If player 1 removes 1 coin from the first pile, the result is (3, 2, 1), which we know is an N-position by part (b).

If player 1 removes 2 (resp. 3) coins from the first pile, the result is (2, 2, 1) (resp. (1, 2, 1)), to which player 2 can respond by removing the coin in the third pile (resp. all coins in the second pile) to give player 1 the P-position (2, 2) (resp. (1, 1)).

This accounts for all of player 1’s possible moves, and all of them lead to N-positions.  We conclude that (4, 2, 1) is a P-position in the variant.

Problem 3

Let A = (Aij) be an m × n payoff matrix for a two-player zero-sum game. Show that

maxminAij  ≤ minmax Aij .

Solution. To start, pick any i,j with 1 ≤ i ≤ m and 1 ≤ j ≤ n. By the definition of max and min, we have

minAij  ≤ Aij  ≤ max Aij .

This is saying that Aij  is bigger than the smallest entry in its column, and smaller than the largest entry in its row.

Now consider the left inequality minjAij  ≤ Aij. This inequality holds for any choice of i, so we can take the maximum over all i to obtain

maxminAij  ≤ max Aij .

To get the final min on the right side, note that the left-hand side is a constant independent of i,j, and that the inequality holds for all j. So we may minimize in j to obtain

maxminAij  ≤ minmax Aij ,

which is what we wanted.                                                                                                                   

Problem 4

Consider the 2 player zero-sum game given by the payoff matrix

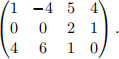
Find the value and optimal strategies for the game.

Solution. The first thing to check when asked to find optimal strategies is whether the payoff matrix has any saddle points. This one does not, so there are no pure Nash equilibria. We now go about finding any mixed Nash equilibria.

We make use of the techniques of domination and mixed domination. First, note that column 4 dominates column 3 for the column player (since the column player wants to minimize losses). Deleting column 3 gives

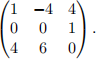
The remaining reductions use mixed domination.   Recall that if we have rows R, R′ , R′′   (resp. columns C, C′ , C′′ ) and constants α,β with α + β = 1 such that αR + βR′  ≥ R′′  (resp. αC + βC′  ≤ C′′ ), in the sense that each entry of the combination is greater than or equal to (resp. less than or equal to) the corresponding entry in the third row (resp.  column), then we can remove R′′  (resp. C′′ ) from the matrix without affecting either player’s strategy.  In the 3 × 3 matrix above, we have

1/2 times row 1 plus 1/2 times row 3 is greater than row 2, so we may remove row 2 to get

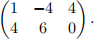
In this matrix, we have 1/2 times column 2 plus 1/2 times column 3 is less than column 1, so column

1 is dominated by the other columns and may be removed. We are left with the 2 × 2 matrix

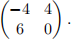
We can now determine theNash equilibria directly. Since neither player has a pure optimal strategy, we can use equalization.  Let (x1 , x2 ) be the row player’s mixed strategy (excluding row 2).  If (x1 , x2 ) is part of a Nash equilibrium then we can equate the column player’s expected losses across both of their possible moves, giving

−4x1+ 6x2 = 4x1 .

Moreover, x1  and x2  add to 1.  So we have two equations in two variables.  Solving the equations gives x1 = 3/7 and x2  = 4/7.

Now we find the column player’s optimal strategy. If (y1 , y2 ) is a mixed strategy for the column player which fits into a Nash equilibrium, we can equate the row player’s expected gains to get

−4y1+ 4y2 = 6y1 .

Since y1 + y2 = 1 also, we get another linear system which we solve to findy1  = 2/7 andy2  = 5/7. The full optimal strategy vectors are then (3/7, 0, 4/7) for the row player and (0, 2/7, 0, 5/7) for the column player.

The value maybe determined by plugging one player’s optimal strategy back in to the expression for expected gain/loss.  For instance, player  1’s expected gain on playing their strategy is 6y1 = 6 · (2/7) = 12/7, so 12/7 is the value of the game.

Problem 5

Suppose I offer a hundred dollar bill to you and your nemesis, with the condition that the two of you have to place bids for it.  In this auction, each of you chooses a multiple of $25 between $0 and $100, and if your bid is the highest, you pay me the bid price for the hundred dollar bill. However, whoever offered the lower bid must pay that amount of money, as well; in a tie, both players pay, but no one receives the $100. Your satisfaction is determined by your net profit minus your nemesis’ net profit.

(a) Write the payoff matrix for this game.

(b) Are any rows/columns dominated by others?

(c) Are there any pure Nash equilibria in this game? If so, find all of them.

(d) Are there any mixed Nash equilibria? If so, find one.

Solution.  (a)  Taking payoff to be the difference of your profits and your nemesis’ profits as re- quested, the payoff matrix for the game is

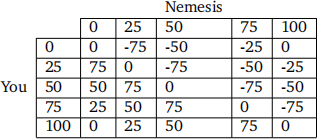
(b) There are rows/columns dominated by the others.   The first row is dominated by the last one, and (noting that the nemesis prefers negative payouts in our setup) the first column is dominated by the last one.  Moreover, the same will be true each time we reduce the matrix via domination in this manner: after removing the first row and column, the remaining first row/column will also be dominated by the last ones.

(c) There is a pure Nash equilibrium in the game. Since pure Nash equilibria correspond to saddle points in the matrix in this situation, we can read offall the pure equilibria directly: this will be the strategy in which both players always bet $100 (bottom-right entry of the matrix).  In particular, the value of the game is 0, which is to be expected since the payoff matrix is skew- symmetric.also go

(d) There is one mixed Nash equilibrium, given by (1/4, 0, 0, 0, 3/4) for both you and the nemesis.

We derive it systematically below, while also showing that no other mixed equilibria exist.

Let x = (x1 , x2 , x3 , x4 , x5 ) be a probability vector giving your strategy in a Nash equilibrium. Writing A for the payoff matrix, each entry of xT A must be greater than or equal to the value 0 of the game. We then have a system

75x2+ 50x3+ 25x4  ≥ 0;

−75x1+ 75x3+ 50x4+ 25x5  ≥ 0;

−50x1 − 75x2+ 75x4+ 50x5  ≥ 0;

−25x1 − 50x2 − 75x3+ 75x5  ≥ 0;

−25x2 − 50x3 − 75x4  ≥ 0;

x1 + x2 + x3 + x4 + x5 = 1.