MATH 110 (Summer 2023) Final Session 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH 110 (Summer 2023)
Final, Session 2
Problem 1 (20 points) Find all triple of integers (x, y, z) such that
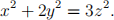
Hint. Find an appropriate rational point that will act as a “pivot”, much like in the case of classifying Pythagorean triples in Lecture 3.8.
Problem 2 Consider the following modular dynamical system, which is neither additive nor multiplicative.
(a) (10 points) Let X = Z/13 and let f : X → X be given by
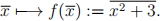
Complete following diagram for the dynamics of f (3 of them have been drawed).
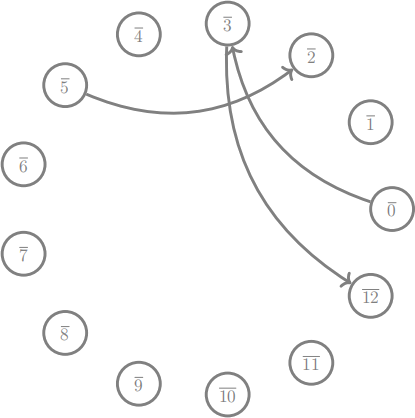
(b) (10 points) Let A0 = 0 and let An+1 = f(An) for all integers n ≥ 0. What is the natural representative of A2023 modulo 13?
Problem 3 (20 points) Consider the following two polynomials modulo 7:

Using the Euclidean Division Algorithm to find a monic polynomial modulo 7 and then show that it is the greatest common divisor of f(T) and g(T) by verifying the two defining properties.
Remark. If you haven’t verified the defining properties, you cannot get the full points.
Problem 4 Determine if the following statements are true or false. If it is true, provide a short justification; if it is false, give a counterexample.
(a) (10 points) If there is an integer x such that x ̸≡ 0 (mod m) but 2x ≡ 0 (mod m), then the modulus m is an even number.
(b) (10 points) If α and β are two Q-linearly independent complex numbers, then α · β is an irrational number.
Problem 5 (10 points) Let p be a prime number and a, b are any nonzero integers such that a ≡ b (mod p 2 − p). Prove that a a ≡ b b (mod p).
Hint. Use Fermat’s little theorem.
Problem 6 (10 points) A place p on Q is either a prime number p or the symbol ∞.
• For the symbol ∞, we will use | · |∞ to denote the usual absolute value | · |.
• For each prime number p, recall the p-adic norm |x| p defined in HW4:

Prove that for any nonzero rational number x, we have
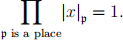
Hint. You need the prime factorization.
Problem 7 Solve the congruence equation x 3 ≡ 21 (mod 208) by following steps:
(a) (10 points) Solve the congruence equation x 3 ≡ 21 (mod 13); more precisely, find all the congruence classes [x]13 that solve the given congruence. Ensure and justify that you have found all the solutions.
Hint. Note that 13 is a prime number. Recall Section 5.4 for the knowledge on modular polynomials, especially those related to the roots.
(b) (5 points) Solve the congruence equation x 3 ≡ 21 (mod 2). Ensure and justify that you have found all the solutions.
(c) (5 points) Lift the solutions in Part b to (mod 4). Ensure and justify that you have found all the solutions of the congruence equation x 3 ≡ 21 (mod 4).
(d) (5 points) Lift the solutions in Part c to (mod 16). Ensure and justify that you have found all the solutions of the congruence equation x 3 ≡ 21 (mod 16).
(e) (5 points) By combining Parts a and c and then applying the Chinese Remainder Theorem, solve the congruence equation x 3 ≡ 21 (mod 208).
2023-09-02