ST302 – Stochastic processes 2021

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

January Assessment 2021

ST302-Stochastic processes

1. Let S=(Sn)n≥o be a simple symmetric random walk. That is,So =0 and for each n≥0,Sn=Yi+Y2+      Yn,where Yi,Y2,.. is a sequence of iid random variables with     P(Yi=1)=     P(Yi=-1)=1/2.Let     Fo     ={0,2}and     Fn=σ(Yi,...,Yn)     for n≥1.

(a)Which of the following processes are martingales with respect to (Fn)n≥o? Justify your answers(if necessary, you can assume that the random vari- ables are integrable).

[6 marks]

(b)  Let  a  <0 and="" b="">0integers  and  define  the  random  timest  =  min{n≥0:  Sn ま(a,b)},Tb=         min{n≥0:Sn         =b}and         g         =max{n ∈[0,1000]:Sn ま (a,b)}. Are T,To and g stopping times? Explain your answer.           [3 marks]

(c)Find the covariance of S, and +(you may need to assume that the optimal sampling  theorem  is  applicable  and  use  the  fact  that  E(T)=-ab  and/or P(S,=a)=b/(b-a)     without     proof).                                              [8 marks]

(d)Find the value of E(To)(Hint: you may need to use the fact that E(T)=-ab). [4 marks]

2.(a) Identify the transient and recurrent states, and the irreducible closed sets for the   Markov   chains   with   the   following   transition matrices.                  |[6 marks]

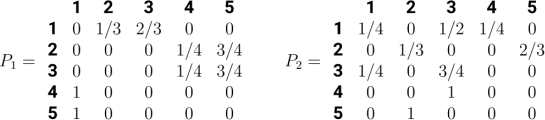
(b)A  particle  moves according to a  Markov chain  in the set  E  ={1,2,..,c,c+  1,...,c+d}. If the particle is in any of the first c states, it jumps to any of the last d states with equal probability in a single step. If the particle is in any of the last d states, it moves to any of the first c states with equal probability in a single step. Show that the stationary distribution is given by

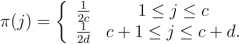
What can you say about the long term behaviour of this Markov chain? Justify your answer.                 [6 marks]

(c)Consider a Markov chain X=(Xn)n≥o with state space E =Z, the set of all integers, and transition probabilities

p(i,i+1)=p

p(i,i- 1)=q,

where0≤p

h(i)=P(Td∈Z.

i. Calculate the value of h(i) for eachi≥ a and show that for anyi≤a-1,

h(i)=h(i+1)p+h(i- 1)q. [3 marks]

ii. Without using Optional sampling theorem, show that

Hint:  Use  telescopic  sums  for  h(a)-h(i)  and  h(0)-h(i)  fori ≤0 and use (without proof) the fact that lim;→-a h(i)=0.                    [6 marks]

3. Let N be a Poisson process withintensityλ> 0 which is adapted to some filtration (Fi)t≥o.Let  Ti,T2,T₃,...  be  its  arrival  times.

(a) Show that Ti conditional on N =1 has uniform distribution on [0,t]. [3 marks]

(b)    For   any   0≤t₁≤t₂≤t,show   that

where fn,r₂ N=2 is the joint density of (Ti,T₂) conditioned on  Ni = 2.Hint: Find     the     joint     probability     P(t₁disjoint.                                    [8 marks]

(c) Assume that λ= 1 and that θ is an exponential random variable with param- eter 1, independent of N. Define the process Y = Not. Show that for any s,t≥0,

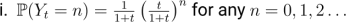
Hint: Condition on θ and you might use the fact that the density of Gamma distribution integrates to one on its domain. [3 marks]

Hint: Use similar reasoning as in part (i).   [3 marks]

iii. Are the random variables Yi and Yi+s-Y independent?   [2 marks]

4. Let B=(Bt)t≥o be a standard Brownian motion.

(a)Show that the following processes can be written as stochastic integrals.

i.X=xexp(at+βB:),withx>0.

ii.Yi     =log(X:).

iii. for0≤t<1. [6 marks]

(b)Solve the SDE

dXt         =B₁Xdt+B;X;dBt,

with Xo = xo.(Hint: Try a solution of the form Xt = exp(Rt), where dRt = Fidt +GidB, for some adapted processes F and G which need to be deter- mined in terms of B.)                  [8 marks]

(c) Use the Feynman-Kac representation result to find a function F(t,x) that solves

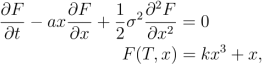
where a, k and a are real constants. You may want to use without proof that for any deterministic function f(t), the  random variable normally  distributed  and  that  if  X～ N(μ,σ²),then  E(X³)=μ³+3μo² . [8 marks]

5.  Let X=(X:)t≥o  be  acontinuous time  Markov  chaintaking values  in  E  ={0,1,2,.} with Q matrix such that Qo,o =0 and forn≥1,

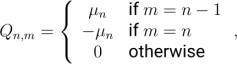
where we have that μn>0 for all n≥1.Denote (Pt)t≥o as the transition probabli- ties    of    this    continuous    Markov    chain.

(a)Write down the Kolmogorov's forward equation and use it to find pr(n,n) for alln>0.                                                                                                           [5 marks]

(b) Determine pt(n,m) in terms of p:(n,m +1) using the Kolmogorov's forward equation and use it to show that for any n≥1,

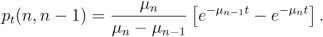[6 marks]

(c)Show  that  if μn =μn,  for  all  n≥0,and  for  some μ>0,then

[6 marks]


2023-08-26