Math 170A Assignment #1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Math 170A Assignment #1
Due date and time: 11pm, August 13, 2023 (PDT)
1. Compute the matrix power A5 for the matrix
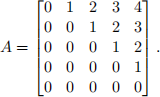
Show all the computational results for A2, A3 , A4 .
Solution:
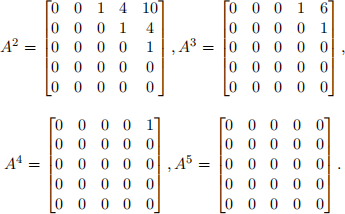
2. Let A = [a1 a2] be a m-by-2 matrix. If X = [x21(x11) x22(x12)], find an
explicit expression for the matrix product AX in terms of a1 , a2 and xij .
Solution: AX = [x11 a1 + x21 a2 x12 a1 + x22 a2].
3. Find all matrices A ∈ R2×2 such that the matrix equation AX = 0 has an invertible matrix solution X ∈ R2×2 .
Solution: Suppose X is an invertible solution of AX = 0. Since X−1 exists, we have
A = A · I2 = A · (XX−1) = (AX) · X −1 = 0.
4. For A ∈ Rnxn , if the equation Ax = bhas a solution for every b ∈ Rn , show that A is invertible.
Solution: Let ei denote the ith column vector of the identity matrix In. Then Ax = ei has a solution xi for all i = 1, 2,...,n. Let X = [x1 x2 ··· xn]. Then
AX = A [x1 x2 ··· xn] = [Ax1 Ax2 ··· Axn] = In.
So X is the inverse of A, i.e., A is invertible.
5. Consider the following lower triangular system
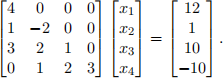
Solve this system by column-oriented forward substitution. Solution: Let us do it with two loops.
(j = 1) b1 = 12/4 = 3.
(i = 2) b2 = 1 — 1 · 3 = —2,
(i = 3) b3 = 10 — 3 · 3 = 1,
(i = 4) b4 = — 10 — 0 · 3 = — 10.
(j = 2) b2 = — 2/( — 2) = 1.
(i = 3) b3 = 1 — 2 · 1 = — 1,
(i = 4) b4 = — 10 — 1 · 1 = — 11.
(j = 3) b3 = — 1/1 = — 1.
(i = 4) b4 = — 11 — 2 · ( — 1) = —9.
(j = 4) b4 = —9/3 = —3.
So we get the solution x + 1 = 3, x2 = 1, x3 = — 1, x4 = —3.
6. Decide the range for the value of t such that the following matrix is positive definite.
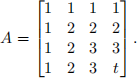
Solution: Observe that A is symmetric, if it is also positive definite, it must have a Cholesky decomposition. After 3 loops of row operations in the Algorithm of Cholesky factorization, the (4 , 4) entry becomes t 一 3. So A is positive definite if and only if t > 3.
7. For A e Rn 根n and X e Rn 根m , if A is positive definite and X has the rankm, show that the matrix product XTAX is also positive definite.
Solution: Since A is positive definite, so xTAx > 0 for all nonzero vector x e Rn. For an arbitrary y e Rm, y ![]() 0, we have Xy
0, we have Xy ![]() 0 since X is full column rank, so
0 since X is full column rank, so
yT (XTAX)y = (Xy)TA(Xy) > 0, Ay ![]() 0.
0.
It implies that XTAX is positive definite.
8. Let A = [A21(A11) A22(A12)] be a 2 根 2 block matrix, for submatrices A11 e
Rn1根n1 , A12 e Rn1根n2 , A21 e Rn2根n1 , A22 e Rn2根n2 . If A is posi- tive definite, show that A11 is invertible and the matrix B := A22 一
A21A11(-)1 A12 is also positive definite.
Proof: Since A is positive definite,
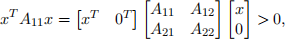
for all nonzero x e Rn1 . So A11 is positive definite, thus it is invertible. For every nonzero y e Rn2 , we have
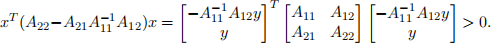
So B is positive definite.
9. Let A = [0 A22(A11 A12)] be a 2 根 2 block matrix, for submatrices A11 e
Rn1根n1 , A12 e Rn1根n2 , A22 e Rn2根n2 . The 0 is a zero matrix of dimension n2 根 n1 . Suppose A11, A22 are invertible. Show that A is invertible and A-1 is a 2 根 2 block matrix of the form
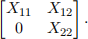
Express Xij in terms of A11, A12 , A22 .
Solution: Let use solve AX = I.
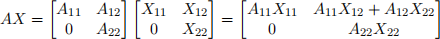
Solving the equations
A11X11 = In1 , A11X12 + A12X22 = 0, A22X22 = In2 ,
we get that
X12 = -A11(-)1 A12A22(-)1 , A11XA22X(12+)22(A1)2X22] X22 = A22(-)1 .
10. Consider the linear system Ax = b, with
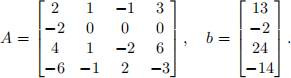
Find a unit lower triangular matrix L and an upper triangular matrix U such that A = LU. Find vectors x,y such that Ly = b and Ux = y.
Solution: By elementary row operations, the matrix A is reduced to
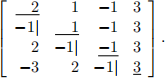
The lower triangular parts sore the multipliers mik . So the factors L,U are
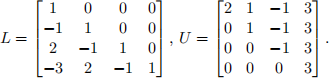
The solution of Ly = b is y = [13; 11; 9; 12]. The solution of Ux = y is x = [3; 2; 3; 4].
2023-08-23
Numerical Linear Algebra