MATH2022 Groups and Vector Spaces Semester One 201920
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH2022
Groups and Vector Spaces
Semester One 201920
1. (i) Give the deinitions of group and abeIian group.
prove that for any integer n > 2, the set z”(*) of members of {1, 2, 3, . . . , n - 1}
which are coprime with n forms a group under the operation of multiplication modulo n. (you may assume without proof that if m and n are coprime, then there are integers x and g such that mx 十 ng = 1.)
(ii) Find which of the following are subgroups of z3(*)0 , giving reasons:
(a) {1, 7, 11, 13}, (b) {1, 7, 13, 19}, (c) {1, 11}.
(iii) prove that if x,g, and 从 are elements of a group G such that xg = xz , theng = z .
(iv) Give an example of a group G and elements x,g, and 从 of G such that xg = zx but g ![]() x .
x .
2. (i) state Lagrange,s Theorem, and from it deduce that any group of prime order is cyclic.
(ii) Deine the direct product of two groups G and H.
(iii) prove that any group of order 4 is isomorphic to z4 or z2 x z2 , but that these two groups are not isomorphic.
(iv) List the right cosets of the subgroup {I, D} of the dihedral group D4 of order 8, whose group table is given.

3. (i) Deine permutation of a set X, and transposition, odd, and even.
prove that the family of all even permutations of a set X forms a normal subgroup of the group of all permutations of X .
(ii) The following permutations f , g in the symmetric group 210 , are given in 2-row notation:
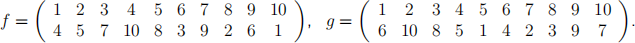
write each off and g as a product of disjoint cycles, and state with reasons which of f , g , f — 1 , g — 1 , fg , gf are conjugate.
(iii) prove that N = {id, (1 2 3), (1 3 2)} is a normal subgroup of 23 , and that H = {id, (1 3)} is a subgroup of 23 which is not normal.
Give a speciic homomorphism from 23 to R* , the group of non-zero real numbers under multiplication, of which N is the kernel. (you do not need to prove that the mapping you deine is a homomorphism.)![]()
![]()
4. (i) Deine IinearIY independent, and spanning subsets of a vector space Ⅴ over a ield F. Deine the dimension of Ⅴ .
(ii) Find a basis of each of the following vector spaces. You do not need to prove that the set you ind is a basis.
(a) The set of solutions of the equations 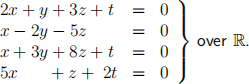
(b) The vector space over c of polynomials p(z) of degree at most 4 with coei- cients in c satisfying p(z) = p(-z) for all z e c andp(-2) = 0.
(iii) Deine the sum U + w of two subspaces U and w of a vector space Ⅴ , and state the circumstances under which this is a direct sum (written U 企 w). prove that if Ⅴ = U 企 w and Ⅴ is inite-dimensional, then dim(Ⅴ ) = dim U + dimw.
5. (i) Find the matrix A of the linear transformation θ from c2 to itself given by
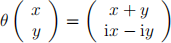 with respect to the basis
with respect to the basis 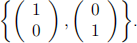
Find the transition matrix P to the basis {u1 , u2 } where 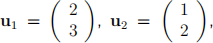 and hence determine the matrix of θ with respect to {u1 , u2 }.
and hence determine the matrix of θ with respect to {u1 , u2 }.
(ii) Determine the eigenvectors and eigenvalues of the real symmetric matrix A =
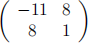 and ind an orthogonal matrix P such that P-1 AP is diagonal.
and ind an orthogonal matrix P such that P-1 AP is diagonal.
(iii) By applying the Gram一schmidt orthogonalization process to the vectors
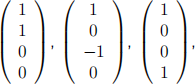 ind an orthonormal basis of the space
ind an orthonormal basis of the space 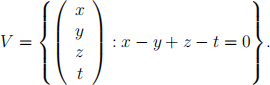
2023-08-22