Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MTH1030 ASSIGNMENT 1

Semester 2, 2023

please submit solutions to the following problems before 5pm on Friday 25 August.  submis- sions maybe handwritten or typed, and details on submission will be provided as we approach the date.

The maximum number of marks is 50, with the number of marks per question indicated below. It is at the discretion of your tutor(s) to deduct up to 10 marks for poor presentation. To obtain  full marks, your assignment should

– be neatly presented, but does not have to be typed;

– not contain any mathematical, logical, spelling or grammatical mistakes;

– be understandable by other students taking the course;

– contain a clear description of the mathematics, with justiication provided in full sentences.

Although we encourage you to initially discuss problems with other students, you must perform your own calculations and write up your assignment independently. Furthermore, any reference to materials outside of what can be found on Moodle, including websites, must be cited clearly. All instances of plagiarism of any nature will be dealt with severely.

unless instructed to do so explicitly, Mathematica and similar software should not be used as part of your solutions. of course, you are welcome to check your own work using a computer. on the other hand, your solution to any question that instructs you explicitly to use Mathematica must include your input and the computer,s output — for example, by inclusion of screenshots.

Question 1. Sequences (13 marks)

(a) prove that the following sequences converge and determine their limits.

Hint. By calculating dn for large n, you can guess the limit L. Then consider dividing dn by L.

Note. Here k is any real number.

(b) Turn the following infinite expression into a sequence and use the monotone bounded sequence theorem to determine its value.

Question 2. series (18 marks)

(a) write down precisely what it means for a series an to be convergent. (This should involve the

notion of a limit, but you do not need the ε deinition of a limit)

write down precisely what it means for a series an to be divergent.                             [1 mark]

(b) write down precisely what it means for a series an to be absolutely convergent.

write down precisely what it means for a series an to be conditionally convergent.     [1 mark]

(c) Determine whether the following series converge or diverge, and ind the limits for those series that converge.

(c) Let c be the last non-zero digit of your Monash student ID number and consider the function f (x) = x) at x = 1. use Mathematica to plot f (x) for 0 三 x 三 2, as well as the Taylor polynomials of degrees 1, 2 and 3 for

f (x) at x = 1.                                                                                                                            [2 marks] Remayk. Approximately one-ninth of you should be pleasantly surprised by your Taylor series!

(d) In the lectures, we deduced that the Taylor series fortan —1 (x) at x = 0 is given by

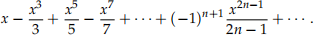
combining this equation with the fact that π = 4 tan —1 (1), we obtain a series for π. use Mathematica to calculate the 1000th partial sum of the series to ten decimal places.  How many of those ten decimal places agree with the decimal expansion of π?      [2 marks]

Question 4. More on harmonic series (6 marks)

(a) The harmonic series diverges very slowly. prove that the sum of theirst 106 terms is less than 15 and that the sum of theirst 109 terms is less than 22. (you should not actually calculate these sums!)                                                              [2 marks]

(b) Determine whether the series is convergent or divergent.                              [2 marks]

(c) prove that the sequence deined by

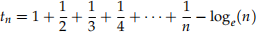
has a limit.                                                                                                                                [2 marks]

Hint. show that tn  > 0 and tn  > tn+1 for all n and then apply the monotone bounded sequence theorem. To prove these inequalities, let yourself be inspired by the arguments and pictures in the section on the integral comparison test from the lectures and lecture notes. what does tn represent pictorially?