MATH1064: Discrete Mathematics for Computation Semester 2, 2023 Assignment 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH1064: Discrete Mathematics for Computation
Assignment 1
Semester 2, 2023
This individual assignment is due by 11:59pm Thursday 24 August 2023, via Canvas. Late assignments will receive a penalty of 5% per day until the closing date. A single PDF copy of your answers must be uploaded in Canvas at https://canvas. sydney.edu.au/courses/44709. It should include your SID. Please make sure you review your submission carefully. What you see is exactly how the marker will see your assignment. Submissions can be overwritten until the due date. To ensure compliance with our anonymous marking obligations, please do not under any circumstances include your name in any area of your assignment; only your SID should be present. The School of Mathematics and Statistics encourages some collaboration between students when working on problems, but students must write up and submit their own version of the solutions. If you have technical difficulties with your submission, see the University of Sydney Canvas Guide, available from the Help section of Canvas.
This assignment is worth 5% of your final assessment for this course. Your answers should be well written, neat, thoughtful, mathematically concise, and a pleasure to read. Please cite any resources used and show all working. Present your arguments clearly using words of explanation and diagrams where relevant. After all, mathematics is about communicating your ideas. This is a worthwhile skill which takes time and effort to master. The marker will give you feedback and allocate an overall mark to your assignment using the following criteria:
1. Show that the following argument with hypotheses on lines 1-2 and conclusion on line c is valid using the rules of inference and logical equivalences. Clearly label each step.
1 p → q Premise
2 (r ∨ s) → (p ∧ ¬q) Premise
. . .
c ¬r Conclusion
2. Decide if the following compound propositions are logically equivalent or not using a truth table. Show your working by including intermediate columns in the truth table.
(p ∧ ¬q ∧ ¬r) ∨ ¬(p ∨ q)
(r → ¬(p ∧ ¬q)) ∧ ¬q
3. Let Q : Z → {true, false} be a predicate with domain Z defined by the statement Q(k) = “k is a non-negative number”.
Let R : Z → {true, false} be a predicate with domain Z defined by the statement R(k) = “k is an even number”.
Let S : Z → {true, false} be a predicate with domain Z defined by the statement S(k) = “k is divisible by 3”.
Determine whether the following statements are true or false. Show all reasoning.
(a) ∀k ∈ Z, Q(k) ∨ Q(−k).
In addition to your answer, write the negation of this statement.
(b) ∀k1, k2 ∈ Z, Q(k1) ∧ Q(k2) → Q(k1 · k2)
(c) ∀k1, k2 ∈ Z, Q(k1 · k2) → Q(k1) ∧ Q(k2)
(d) ∀k1, k2 ∈ Z, R(k1) ∧ S(k2) → R(3k1 + 2k2) ∧ S(3k1 + 2k2)
(e) ∀k1, k2 ∈ Z, R(k1) ∨ S(k2) → R(3k1 + 2k2) ∨ S(3k1 + 2k2)
(f) ∃k1, k2 ∈ Z : R(3k1 + 2k2) ∧ ¬R(k1).
In addition to your answer, write the negation of this statement.
(g) There exists a k ∈ N : R(k) ∧S(k) is true, and for all ` > k, ¬(R(` ) ∧S(` )) is true.
4. Suppose we have a circle that has radius r = 1 unit, and that we label five distinct points in the circle (or on the edge), with the set of points given by P = {p1, p2, p3, p4, p5}.
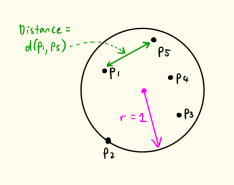
Let the distance between points pj and pk be written as d(pj , pk). Use the pigeonhole principle to show
∃pj , pk ∈ P : (j = k) ∧ (d(pj , pk) < √ 2).
2023-08-18