MATH2001/7000 ASSIGNMENT 1 SEMESTER 2 2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH2001/7000 ASSIGNMENT 1
SEMESTER 2 2023
Due at 5:00pm 18 August. Marks for each question are shown. Total marks: 25
Submit your assignment online via the assignment 1 Gradescope submission link in Black-board.
(1) (4 marks.) You are given that the ODE
2xy + (y2 − 3x2 )y' = 0
is almost exact, i.e. there exists an “integrating factor” h(y) such that
2xyh + (y2 − 3x2 )h y' = 0
is exact. Find the integration factor h(y) and use your result to obtain the general solution of the almost exact ODE.
(2) (4 marks.) Find the general solution of the ODE
y'' + 2y' + 2y = e−x (1 + cos x).
(3) (5 marks.) Let β = {e1, e2, e3} be a basis of P2(R), where e1 = x − 1, e2 = x + 1, e3 = x 2 + 3. Find the coordinate vector of v = x 2 + x relative to β and show that {e1, e2, v} is a basis for P2(R).
(4) (4 marks.) Let the solution space U of the system of equations
2x1 + x2 + 3x3 − x4 + x5 = 0,
3x1 + 2x2 − 2x4 + x5 = 0,
3x1 + x2 + 9x3 − x4 + x5 = 0,
be the subspace of R 5 endowed with the usual dot product. Find a basis for U and a basis for the orthogonal complement U ⊥.
(5) (8 marks.) Let  and define
and define
(a) Show h A, Bi is an inner product of M2,2(R).
(b) Find an orthonormal basis for the subspace U of M2,2(R) spanned by
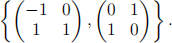
2023-08-18