Homework Problems for Chapter 7
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Homework problems for chapter 7
7.1 comparing various methods
solve the linear system with the four methods below (Do not use Matlab).
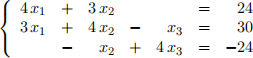
(a). Gaussian elimination (tridiagonal system).
(b). Jacobi,s method.
(c). Gauss-seidel,s method.
(d). The sOR-method, with w = 1.25.
For the methods in (b), (c) and (d), write out the general iteration scheme, then do 2 iterations for each method, with initial guess
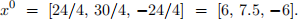
Among the methods (b), (c), (d), which seems to work better for this example? please comment.
7.2 More practice on various methods
Do not use Matlab for this problem.
consider the system of linear equations
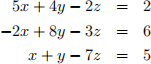
. perform one step Jacobi iteration, using x0 = g0 = 从0 = 1 as starting value.
. perform one step Gauss-seidel iteration, using x0 = g0 = 从0 = 1 as starting value.
. Do Jacobi iterations converge for this system? Do Gauss-seidel iterations converge for this system? why?
(a). write a Matlab function which solves a system of linear equations Ax = b, with successive over relaxation (SOR) iterations. Assume here that A is a banded matrix with bandwidth d, (so that aij = O for |i -j| > d). The inputs of the function are: A, b, a starting vector x0, the band-width d, the relaxation parameter 山, an error tolerance ε and the maximum number of iterations. The iteration stops when the error (you may use the residual T = Ax -b measured in certain norm) is less than the tolerance, or when the maximum number of iterations is reached. The function should return the solution vector x and the number of iterations.
The irst few lines in the function should look like this:
function [x,nit]=sor(A,b,xo,w,d,tol,nmax)
X SOR : solve linear system with SOR iteration
X Usage: [x,nit]=sor(A,b,xo,omega,d,tol,nmax)
X Ⅰnputs:
X A : an n x n-matrix,
X b : the rhs vector, with length n
X xo : the start vector for the iteration
X tol: error tolerance
X w: relaxation parameter, (1 < w < 2),
X d : band width of A .
X Outputs::
X x : the solution vector
X nit: number of iterations
(b). use your function sor to solve the following tridiagonal system, with
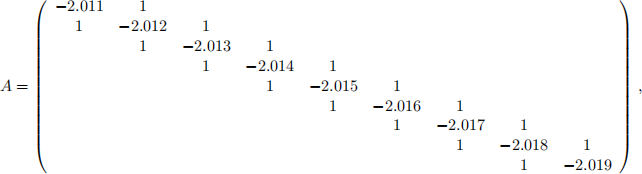

Here bis the load vector and x0 is the initial guess. Solve the system with an error toler- ance E = 1O-4 , setting 1OO as the maximum number of iterations. Try diferent values of w between 1 and 2 (this is called over-relaxation), for example w = 1.O)1.1)1.2). . . )1.9. Search for the value of w that gives the fastest convergence (requiring the smallest number of iterations). Make a plot of number of iterations as a function of w.
what to hand in? your Matlab ile sor.m, the script, the running result, the plot, and whatever comments you have.
7.4 Jacobi iterations in Matlab
write a Matlab function, using Jacobi,s method to solve a system of linear equations. Do it similarly as in the Matlab problem for SOR, but only for tri-diagonal systems.
Test it on the same system in problem 2b), with error tolerance E = 1O-4 and setting the maximum number of iterations =1OO. compare the result with the result from SOR. which method converges faster? put your comments.
what to hand in? your Matlab ile 二acobi.m, the script, the running result, and whatever comments you have.
7.5 SoR with Jacobi iterations
(a). Design an SOR method based on Jacobi iteration. write out the iteration step,
i.e., the formula to compute xi(k)+1 for (i = 1). . . )n) when given xi(k) for (i = 1). . . )n).
(b). write the matrix formula for this SOR method.
7.6 symmetric Gauss-seidel Method
(a). Design asymmetric Gauss-seidel method, which does 2 sweep with diferent order of variables in the inner for-loop. To be precise, for each iteration step k, we irst carry out the computer from i = 1 to i = n in the increasing direction of the index, then we carry out the computer from i = n to i = 1 in the decreasing direction of the index. write out the details of the iterations.
(b). write this method in matrix-vector form.
(c). code this in Matlab. Test it on the system in Example of chapter 7.5 in the textbook, and compare the performance. Make your comments.
2023-08-12