MATH3301-WE01 Mathematical Finance III 2021
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH3301-WE01
Mathematical Finance III
2021
Q1 consider the following 2-period Binomial market shown as a tree.
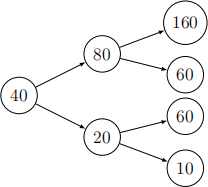
The interest rate is 3/4. Answer the following questions and show your work.
1.1 calculate the martingale probabilities along the edges of the tree.
1.2 consider the contingent claim X = So + S1 - S2. calculate the arbitrage-free price of X at time 0.
1.3 Explain in words the meaning or signiicance of the price of X from part 1.2. Let (wt , t > 0) be a Brownian motion started at wo = 0.
1.4 use It“o,s formula to show that if h : R 一 R is diferentiable, then

Deine Go := 0, and, fort 持 0, Gt := t-1 1o(t) ws ds. Also let yt := wt - Gt fort > 0.
1.5 show that Gt … Ⅵ (0, σt(2)) and yt … Ⅵ (0, σt(2)), where σt(2) is a function of t > 0 that you should determine.
1.6 Find cov(Gt , yt ).
1.7 Do (Gt , t > 0) and (yt , t > 0) have the same distribution as processes? Explain briely.
Q2 consider a market consisting of two periods t = 0 and T, a stock St and interest compounded continuously at rate T . Assume the market has no arbitrage. There are two contingent claims X and Y as follows.
claim X: At time t = T the holder of the claim has the right, but not the obligation, to buy 1 unit of the stock for a strike price K. If the holder does not exercise the option to buy the stock, then the holder has to pay a penalty of price J.
claim Y : At time t = T the holder of the claim has the right, but not the obligation, to sell 1 unit of the stock for a strike price K. If the holder does not exercise the option to sell the stock, then the holder instead gains an amount J.
2.1 show, with proper explanation, that the value of X at time T is max{ST - K, -J} and the value of Y at time T is max{K - ST , J}.
2.2 Let C be the price of X at t = 0 and P be the price of Y at t = 0. prove that P + S0 = C + (K + J)e-rT .
2.3 prove or disprove whether the following inequalities hold for every value of J and K:
(i) P < S0 ; (ii) C < S0 .
You must explain your reasoning.
Q3 consider a market w = (Bt , St ) consisting of a bond and a stock as follows for t = 0, T.
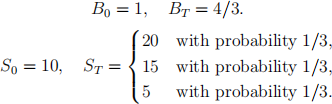
A portfolio in this market is a vector h = (x, g) E R2. The value of the portfolio h is Ⅴth = xBt + gSt fort = 0, T.
3.1 The market contains arbitrage if there is a non-zero portfolio h such that
Ⅴ0h = 0, ⅤT(h) > 0 with probability 1 and ⅤT(h) > 0 with positive probability.
prove that this market contains no arbitrage.
3.2 A portfolio h is replicating for a contingent claim x if ⅤT(h) = x almost surely.
consider the following two contingent claims x1 and x2 .
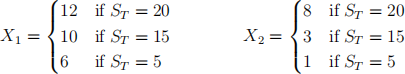
For each of x1 and x2 , either ind a replicating portfolio or prove that none exists. Show your work neatly.
3.3 consider the contingent claim x1 from part 3.2. Find the arbitrage-free price of x1. Justify your answer.
3.4 A martingale measure for this market is a change of measure Q on the stock ST such that under Q the following identity holds:
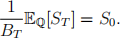
Find, with proper justiication, all martingale measures in this market.
Q4 Suppose that (xt , t > 0) is an It^o process with x0 = x0 > 0, xt > 0 for all t > 0, satisfying the stochastic diferential equation (SDE)
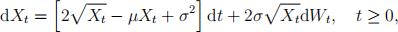
where (wt , t > 0) is a Brownian motion and μ E R and σ > 0 are constants.
4.1 For a E R, let yt = eμt/2xt(a) . Derive an SDE for yt (you may leave the right-
hand side in terms of xt ). There is a special value a = a* for which the drift in the SDE for yt is deterministic. what is a*?
4.2 Solve the SDE for yt that you obtained in question 4.1 in the special case
a = a* . Hence ind an expression for xt(a)* .
4.3 calculate E(xt(a)* ) and var(xt(a)* ). carefully justify your calculations.
4.4 Find limt一必 E(xt ); you should consider the cases μ < 0, μ = 0, and μ > 0.
Q5 consider the continuous-time Black—scholes market, with price dynamics given by
dBt = TBt dt, dst = μst dt + σst dwt ,
where T > 0 is the risk-free interest rate, μ and σ are constant parameters, and (wt , t > 0) is a Brownian motion under the real-world measure P.
A contingent claim XT with expiry time T and threshold K > 0 is given by
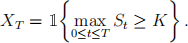
5.1 show that the arbitrage-free price Ⅱ0 (XT ) at time 0 of XT can be expressed in terms of an expectation under the risk-neutral measure Q satisfying
EQ [XT ] = H(T, a, g),
where a, g are functions of s0 , K, σ, and T , and

5.2 By considering a change of measure under which (at+wt , t > 0) is a Brownian motion, show that the probability in (1) can be written in terms of
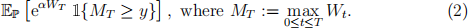
Give a careful explanation of the application of any theorem from lectures that you use.
5.3 Take T = 1. It can be shown that the joint distribution of w1 and M1 is given by
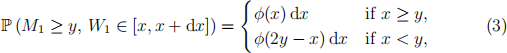
where φ is the standard normal density function. use (3) to compute (2) and hence determine Ⅱ0 (X1 ). your answer may be written in terms of N(x), the cumulative distribution function of the standard normal distribution.
5.4 Give a brief explanation of the origin of formula (3).
2023-08-11