Midterm 3: Math 124 Summer 2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Midterm 3: Math 124 Summer 2023
Due: Midnight, Monday 7/24/2023, at Gradescope
Instruction: You must type your solution using LaTeX. Explain your solution. Answers without explanation may not receive credits. Clarity and precision of your writing is part of your scores. Your solution is your first draft. Reread it and correct your English. You can attach a scanned picture to your PDF file.
[1] (3+5+5+7=20 points) A plane model of a surface is given by the following word:
aba−1 ecdb−1 d −1 ec−1 .
(1) Is the surface orientable or nonorientable? Explain.
(2) The above word induces a cell decomposition on the surface. Find the number of vertices v, the number of edges e and the number of faces f in this cell decomposition. Then, compute the Euler characteristic of this surface.
(3) Identify this surface as gT or hP.
(4) Use circulation rules to completely transform this word into the standard form. In-dicate rules you used.
Solution. (1) The surface is non-orientable, since the letter e repeats in the word.
(2) You can draw a graph of vertex identification to check that there are 2 vertices in the induced cell decomposition on the surface. Since there are 5 letters in the word, there are five 1-cells (edges). For a cell decomposition induced by a word, the number of 2-cells is always 1. So the Euler characteristic of the surface is χ − 2 − 5 + 1 = −2.
(3) Since the surface is non-orientable, compact, and without boundary, it is homeomorphic to a genus h non-orientable surface hP for some h. To determine h, we note that χ(hP) = 2 − h. Since the surface in question has χ = −2, we have h = 4. Hence the surface is 4P.
(4) Since the word is non-orientable, we use the M¨obius rule repeatedly. Another rule which may be needed is that we can apply cycle rule or flip rule to a surface block in a word.
aba−1 ecdb−1 d −1 ec−1 ∼ aba−1 eedbd−1 c −1 c −1 (M¨obius rule applied to e)
∼ abbd−1 e −1 e −1 ad−1 c −1 c −1 (M¨obius rule applied to b)
∼ aaeedb−1 b −1 d −1 c −1 c −1 (M¨obius rule applied to a)
∼ aaeeb−1 b −1 d −1 dc−1 c −1
(Cycle rule applied to a surface blockdb−1 b −1 d −1 )
∼ aaeeb−1 b −1 c −1 c −1 (Sphere rule applied to d −1 d).
[2] (5+10+5+5=25 points) Let X be the compact connected surface spanning the following knot. Let X∗ be a surface without boundary obtained by gluing a disc to X along its boundary.
(1) Is X orientable? Explain.
(2) Find the Euler characteristic of X by introducing a suitable cell decomposition of X.
(3) Find χ(X∗ ).
(4) Identify X∗ as nT, mP.

Solution. (1) Note that every time the surface goes through the knot crossing, it goes through a half twist. Since there is a simple closed curve on the surface which goes through three half twists, the surface is non-orientable.
(2) We appropriate cuts so that the surface breaks up into pieces homeomorphic to discs. For example, we can cut the surface near each half twist. If there are k crossings in the knot, then we introduce k cuts near the crossings. This result in 2k vertices and 3k edges. If f is the number of resulting pieces of the surface homeomorphic to discs, then the Euler characteristic is given by χ = k − 2k + f = f − k. Since there are 8 crossings and 8 cuts results in 5 pieces of surfaces homeomorphic to discs, we have χ = 5 − 8 = −3.
(3) Since X has one boundary circle (=knot), the capping this boundary increases the Euler characteristic by 1. So χ(X∗) = χ(X) + 1 = −2.
(4) Since the surface X∗ is compact non-orientable surface without boundary with χ = −2, and since χ(hP) = 2 − h, we have h = 4.
[3] (4 points each, 24 points) Thicken the following loops on the Klein bottle.
(1) Decide whether they are cylinders or M¨obius bands. Explain.
(2) Cut the surface by each of these curves (not simultaneously). What are the resulting surfaces for three cases?
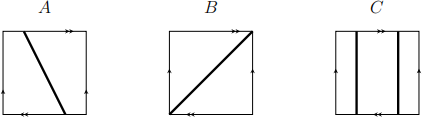
Solution. See explanation on the solution of midterm 2. Here, we only give answers.
(1) In cases A, B, we get M¨obius bands. In case C, we get a cylinder.
(2) Do cup-and-paste. In cases A, B, we get one M¨obius band in each case. In case C, we get two M¨obius bands.
[4] (15 points) A convex polyhedron with only triangle faces and square faces has a property that at each vertex, 2 triangles and 2 squares meet. Compute the number of vertices, edges, triangle faces, and square faces. (Hint: Let f3 and f4 be the number of triangles and squares. Count the number of pairs (triangle, a vertex on it) in two ways. Do the same for squares. Also, write down other standard equations.)
Solution. Let f3 and f4 be the number of triangles and squares. Then f = f3 + f4. Since the valency of every vertex is 4, we have 2e = 4ν. The Euler characteristic formula gives ν − e + f3 + f4 = χ = 2. Here, the solid polyhedron means that the surface is a sphere. So χ = 2. The face-edge formula gives 2e = 3f3 + 4f4. We have 4 unknowns ν, e, f3, f4 and three equations. We need one more equation. The condition we have not used is that at each vertex, two triangles and two squares meet. We count the number of pairs (triangle, a vertex on it) in two ways. For each vertex, by hypothesis, it is on two triangles, and there are ν vertices. So there are 2ν pairs. On the other hand, for each triangle, there are three vertices on it, and there are f3 triangles. Hence there are 3f3 pairs. Hence 2ν = 3f3. Similarly, we have 2ν = 4f4 by counting the number of pairs (square, a vertex on it). By solving this system of equations, we find ν = 12, e = 24, f3 = 8, f4 = 6.
[5] (5+5+5=15 points) Prove the following spatements.
(1) Show that a closed subset of a compact space is compact.
(2) Show that a compact subset of a Hausdorff space is closed.
(3) Prove that a continuous map f : X → Y from a compact space X to a Hausdorff space Y is closed, that is, for every closed subset V of X, its image f(V ) is a closed subset in Y .
Solution. Let V is a closed subset of a compact space X.
(1) We show that a closed subset of a compact space is compact.
To see this, let V be a closed subset. Let {Uα} be an open cover. Then {Uα} ∪ {X − V } is an open cover of X. Since X is compact, this open covering has a finite open subcover. By discarding the open set X − V from this finite subcover, we see that V admits a finite sopen ubcover. Hence a closed subset of a compact space is compact.
Since the continuous image of a compcat set is a compact set f(V ) is compact.
(2) We show that a compact subset in a Hausdorff space is closed.
Let A be a compact subset of a Hausdorff space X. In Midterm 1 problem [5], we showed that for any point x ∈ X not in A, here exists an open neighborhood Ux disjoint from A.
Then

is an open subset of X. Hence A is closed.
(3) Let V be a cloed subset of a compact space X. Then by (1), V is compact. Since the continuous image of a compact set is compact, f(V ) is compact in Y . Since Y is Hausdorff, its compact subset f(V ) is closed. Hence f is a closed map.
2023-07-29