Midterm 2: Math 124 Summer 2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Midterm 2: Math 124 Summer 2023
Due: midnight, Monday 7/17/2023, at Gradescope
Instruction: You must type your solution using LaTeX. This is a take-home exam and you can use textbooks, your class notes, references, etc., but you cannot collaborate with other students. You have three and a quarter days to complete this assignment. Clarity and precision of your writing is part of your scores. Your solution is your first draft. Reread it and correct your English. No late submission will be accepted.
[1] (8+12=20 points) Identify the following surfaces as S 2 , Σg = gT, or Nh = hP, with g, h ≥ 1. Explain. Here a circle with two arrows in the same direction indicate the result of removing an open disc and identifying antipodal points along the resulting boundary circle. In the second picture, the actual surface does not have self-intersections.

Solution. For the first one, move the handle continuously to the side, and we see that we have an orientable surface with 8 holes, that is, 8T. For the second surface, it is a connected sum of two Klein bottle, two tori, and two projective plane. Using P#T ∼ = 3P, we have 2K#2P#2T ∼ = 10P.
[2] ((4+10)+(4+10)=28 points) The S1 and S2 be surfaces whose plane models are given by words M1 and M2 given below.
M1 = abcdf −1 d −1 fg−1 cgee−1 b −1 a −1 , M2 = aba−1 ecdb−1 d −1 ec−1
For each of these surfaces, answer the following questions.
(1) Is the surface orientable? Explain your reason.
(2) Use circulation rules to transform each word into a standard form, and identify each surface as nT, or mP. Show all of your work.
Solution. For M1:
(1) The word c repeats twice. Hence the surface is nonorientable.
(2) First, use the cycle rule to move ab at the front to the back. Then use sphere rules to cancel ee−1 , a −1a and b −1 b. Apply M¨obius rule to the letter c, then to letter g to get ccggdf −1d −1 f. Note that this word represents P #P #T. To go further, we apply the cycle rule to the suyrface block after cc to get ccfggdf −1d −1 . Now apply the cylinder rule to f · · · f −1 to get ccfgdgf −1d −1 . Now apply M¨obius rule to g to get ccfggd−1 f −1d −1 . Now apply the cylinder rule to the surface block after cc to move f to the end: ccggd−1 f −1d −1 f. Then M¨obius rule applied to d −1 gives ccggd−1d −1 ff, which is the word for 4P.
For M2.
(1) The surface is non-orientable, since the letter e repeats in the word.
(2) Since the word is non-orientable, we use the M¨obius rule repeatedly. Another rule which may be needed is that we can apply cycle rule or flip rule to a surface block in a word.
aba−1 ecdb−1 d −1 ec−1 ∼ aba−1 eedbd−1 c −1 c −1 (M¨obius rule applied to e)
∼ abbd−1 e −1 e −1 ad−1 c −1 c −1 (M¨obius rule applied to b)
∼ aaeedb−1 b −1 d −1 c −1 c −1 (M¨obius rule applied to a)
∼ aaeeb−1 b −1 d −1 dc−1 c −1
(Cycle rule applied to a surface blockdb−1 b −1 d −1 )
∼ aaeeb−1 b −1 c −1 c −1 (Sphere rule applied to d −1 d).
[3] ((6 + 6) × 3 = 36 points) Consider the following loops on the Klein bottle.
(1) Decide whether they are orientation reversing or preserving. Explain.
(2) In each of the three case, cut the surface by the curve. What is the resulting surface for each case?
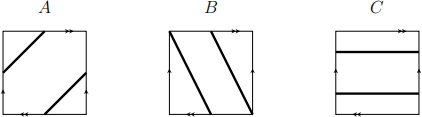
Solution. (1) A curve on a surface is orientation preserving (reversing) if the thickened strip on the surface is a cylinder (M¨obus band, respectively). A more convenient way to decide is the following. In general, in a plane model of a surface, call an edge a non-orientable if a appears in the same direction (· · · a · · · a · · · or · · · a −1 · · · a −1 · · · in the word). Then the curve is orientation preserving if it crosses non-orientable edges even number of times, and the curve is orientation reversing if the curve crosses non-orientable edges odd number of times.
Thus, the curve in A is orientation reversing, and the curves in B, C are orientation preserving.
(2) We do cut-and-paste. A gives a M¨obius band. B gives two M¨obius band. C gives two cylinders.
[4] (4 × 5 = 20 points) Let A = {0} ∪ { 1k | k ∈ N} ∪ [1, 2) with the subspace topology from R 1 .
(1) Is [1, 3 2 ) open, closed, or neither in A?
(2) Is { 1 k | k ∈ N} open, closed, or neither in A?
(3) Is { 1 k | k ≥ 2} open, closed, or neither in A?
(4) Is {0} open, closed, or neither in A?
(5) Is { 1 k } for some k ∈ N open, closed, or neither in A?
Solution. (1) Open, but not closed.
(2) Neither.
(3) Open, but not closed.
(4) Closed, but not open.
(5) For k > 1, {1/k} is both open and closed. The set {1} is closed, but not open.
[5] (10 points) Prove that an infinite subset of a compact space has a limit point. Solution. See the proof of Bolzano-Weierstrass theorem in textbook.
2023-07-29