Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MAST30021 Complex Analysis

Assignment 1 (S2 2021)

Marks will be deducted in every question for incomplete working, incorrect use of mathematical notation and insufficient justification of steps. Please start working on this assignment as early as possible and attempt to finish it way ahead of the deadline. Even though you have two weeks to work on these problems, they might turn out to be longer and more involved than initially expected. Also, take into account that some time is required to scan and upload your solutions. Note that some questions may require a definition to be given later in the Lectures.

Expected level of rigour

● Problems will be clearly marked as “computational” or “proof”.

● In “computational” questions the focus is on the computation or result and, while justifications need to be given, it is sufficient to show a sense of awareness of the underlying mathematical issues, refer to limit laws etc. Example: “An open square S is open since each of its points has a non-zero distance to the boundary” would be adequate for a “computational” question.

● In “proof” questions you are expected to provide full and rigorous justifications, written in mathematically appropriate terms. Example: The statement above would not be adequate for a “proof question”. You would need to specify the distance to the boundary explicitly and show the existence of a neighbourhood that is fully contained in S.

● In either case it is usually not sufficient to only write mathematical formulas or symbols. Your answer should contain text that clearly explains what is going on. You are allowed (and encour-aged) to use results from lecture slides, problem sheets or earlier assignments but these need to be named or referenced appropriately. Lack of logical coherence will lead to the deduction of marks even if the computation or proof idea is generally correct.

Late or missed assignments

● Students unable to submit assignments due to illness or other extenuating circumstances may receive sympathetic treatment, provided that the circumstances are significant and supported by appropriate documentation. Sympathetic treatment will normally mean excusing the stu-dent from submitting the assignment and adjusting the weights of the assessment components appropriately.

● Any medical certificates relating to the assignments should be given to the coordinator as soon as possible after the piece of assessment is due.

● If you are working on your assignment up to the last possible submission time, it is likely that you will not be keeping up with current topics, which can have bad e↵ects on your overall performance. Early submission before the deadline is strongly encouraged.

● In view of the above arrangements, there are no circumstances under which extensions of time will be granted and students are strongly advised against waiting until the last possible minute before submitting their assignment. Assignments submitted after the due date will not be marked.

Concerning plagiarism

● Please familiarise yourself with the University’s expectations on Academic Integrity. Note, in particular: You are expected to submit work that is original and solely your work, without assistance by any other person (collusion).

● Detected plagiarism or other forms of academic misconduct may lead to serious disciplinary consequences for students involved.

Question 1: Lecture Summary (10 marks)

Write a summary of the lecture material for each of the weeks 1-3, using up to one A4 page per week.

Your summary can contain tables, diagrams, pictures etc—try to design it so that it would be useful when explaining the material to another person and/or when preparing for the exam. It must be hand-written on the template provided at the end of this assignment (yes, it’s just one A4 page per week). There must be at most one line of your summary text per one line on the template. Any person with normal eyesight should be able to read your summary without the help of a magnifying glass or any other optical/electronic device. The point is not to give a complete account but rather to identify the most important aspects of the lecture material.

Question 2: Simple proofs (10 marks)

1. Let  be a set that contains one or more boundary points. Show that S cannot be open.

2. Let  be a set that is contained in the open disc . Show that this set is bounded (according to the definition given in the lecture).

3. Let be a subset of the complex plane. Show the equivalence of the following two state-ments:

(a) The set S is unbounded (i.e. not bounded).

(b) The point  is a cluster point of S.

Question 3 - Simple computations (10 marks)

(a) Compute the following limit if it exists.

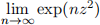
In case the limit does not exist characterise the type of divergence. Note that the result may depend on the choice of . Illustrate your results by drawing a z-plane and labelling different regions or parts appropriately.

(b) Let C be the circle of radius 2 centred at (with anti-clockwise orientation). Compute the integral

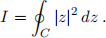
Remember that you are expected to provide detailed justifications.

Question 4 - Part A: Advanced computation (10 marks)

You are only required to submit one part for Question 4 and correspondingly only one part will be marked. If you submit both parts please indicate which one should be marked as otherwise the tutor will make a decision at their own discretion.

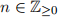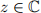Let and with .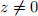

(a) For show that

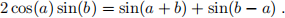
(b) Establish the validity of the following formula

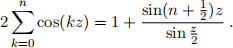
(c) Use the result of part (b) to compute the limit

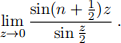
Question 4 - Part B: Advanced proof (10 marks)

You are only required to submit one part for Question 4 and correspondingly only one part will be marked. If you submit both parts please indicate which one should be marked as otherwise the tutor will make a decision at their  own discretion.

Let 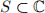be a punctured neighbourhood of 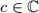and consider a function 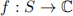defined on that set.

(a) Show that c is a cluster point of S.

(b) Prove the equivalence of the following two statements:

(i) Given there exists a such that whenever .

(ii) If is an arbitrary sequence of points with as , then as .

In other words, your proofs establish the equivalence of the two definitions given on pages 4 and 5 of Lecture 4 (whenever both apply).