COMP3121/9101 23T2 — Assignment 3
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COMP3121/9101 23T2 — Assignment 3
Due Friday 28th of July at 6pm Sydney time (week 9)
In this assignment we will apply dynamic programming. There are three problems each worth 20 marks, for a total of 60 marks. Partial credit will be awarded for progress towards a solution. We’ll award one mark for a response of“one sympathy mark please”for a whole question, but not for parts of a question.
Any requests for clariication of the assignment questions should be submitted using theEd forum. We will maintain a FAQ thread for this assignment.
For each question requiring you to design an algorithm, you must justify the correctness of your algorithm. If a time bound is speciied in the question, you also must argue that your algorithm meets this time bound. The required time bound always applies to the worst case unless otherwise speciied.
You must submit your response to each question as a separate PDF document on Moodle. You can submit as many times as you like. Only the last submission will be marked.
Your solutions must be typed, not handwritten. We recommend that you use LaTeX, since: . as a UNSW student, you have a free Professional account on Overleaf, and
. we will release a LaTeX template for each assignment question.
Other typesetting systems that support mathematical notation (such as Microsoft Word) are also acceptable.
Your assignment submissions must be your own work.
. You may make reference to published course material (e.g. lecture slides, tutorial solutions) without providing a formal citation. The same applies to material from COMP2521/9024.
. You may make reference to either of the recommended textbooks with a citation in any format.
. You may reproduce general material from external sources in your own words, along with a citation in any format.‘General’here excludes material directly concerning the assignment question. For example, you can use material which gives more detail on certain properties of a data structure, but you cannot use material which directly answers the particular question asked in the assignment.
. You may discuss the assignment problems privately with other students. If you do so, you must acknowledge the other students by name and zID in a citation.
. However, you must write your submissions entirely by yourself.
– Do not share your written work with anyone except COMP3121/9101 staf, and do not store it in a publicly accessible repository.
– The only exception here is UNSW Smarthinking, which is the university’so伍cial writing support service.
Please review the UNSW policy on plagiarism. Academic misconduct carries severe penalties.
Please read the Frequently Asked Questionsdocument, which contains extensive information about these assignments, including:
. how to get help with assignment problems, and what level of help course staf can give you . extensions, Special Consideration and late submissions
. an overview of our marking procedures and marking guidelines
. how to appeal your mark, should you wish to do so.
Question 1
You are travelling with your friends along the Geraldton coast with cities c0 , c1 , c2 , . . . , cn on the shore. You are starting in city c0 where a famous spa is, and need to reach the airport situated in city cn , so you will visit each city c0 , c1 , c2 , . . . , cn in that order.
In each city you may swap the animal you are riding on and the choices are a girafe, a mammoth, an ant, an iguana, and a lemur, denoted G, M, A, I, L respectively. However, each city has its own rules what kind of animal exchanges are allowed. For example, in some of the cities you can swap a girafe only for a lemur or an ant (and you cannot remain on your girafe), in others you can swap a mammoth only for a girafe or decide to remain on your mammoth, and so on. You know all the rules of all the cities c1 , . . . , cn , expressed by a function R(i, a, b) where R(i, a, b) = 1 if in city ci one can swap animal a for animal b, and zero otherwise (a and b belong to the set {G, M, A, I, L}, and 1 ≤ i < n). You also know the speed v(a) in km/h (a ∈ {G, M, A, I, L}) of each of the ive animals, as well as the distances d(i) in km between cities ci−1 and ci for all i = 1, 2, . . . , n. Calculating a given value of R, v, or d can be done in O(1) time.
You may begin your journey from c0 on any of the ive animals. You need to choose which animals to use for each of the n trips between cities, such that your travel time is minimised and every animal swap is valid.
1.1 [2 marks] Consider the case of n = 2, with d(1) = 1, d(2) = 3, and v deined as
v(G) = 7, v(M) = 3, v(A) = 2, v(I) = 1, v(L) = 4.
Deine R so that
R(1, G, M) = 1, R(1, A, M) = 1, R(1, A, A) = 1, R(1, I, G) = 1, R(1, L, I) = 1,
and R(1, a, b) = 0 for all other values of a, b.
Determine which animals you should choose on each trip in order to minimise the total time taken to travel from c0 to c2. You must justify your selection.
1.2 [12 marks] Design an algorithm which determines the minimal amount of time (in hours) it will take to get from c0 to cn without making invalid swaps, as well as the animals required on each trip to achieve this time. Your algorithm must run in O(n) time.
1.3 [6 marks] While planning your trip, your friend Mae points out that animals are living creatures, and do, in fact, need to rest. To take this into consideration, you estimate the efect of consecutive trips on the animals, and come up with a magical constant, 0 < ε < 1. For each consecutive trip an animal makes, the speed of the animal is multiplied by this constant.
For example, if you decide to travel on a mammoth from c0 to c1 to c2 to c3 without ever changing animals, then the mammoth’s speed will be v(M) from c0 to c1 , εv(M) from c1 to c2 , and ε2 v(M) from c2 to c3. Of course, if you then swap animals, and later decide to travel by mammoth again, the new mammoths are not tired, and thus have speed v(M). You may not“swap”an animal for “new”animals of the same type.
Design an algorithm which determines the minimal amount of time (in hours) it will take to get from c0 to cn without making invalid swaps. Your friends are judging you for not considering this in the irst place, so your algorithm must run in O(n2 ) time before things become more awkward.
Question 2
You are given a string w = w1 w2 . . . wn of n letters that come from a ixed alphabet. A palindrome is a substring w′ such that w′ can be read the same forwards and backwards. For example, w′ = kayak forms a palindrome while w′′ = kayaak does not form a palindrome. A palindromic substring is a contiguous subsequence of w that forms a palindrome.
2.1 [8 marks] We want to eventually ind a minimum cost decomposition of w into palindromes. However, to do this, we need to irst ind where the palindromes are. Given a string w = w1 . . . wn , describe an O(n2 ) algorithm to identify all of the palindromic substrings of w.
|
Hint. How many subproblems can you have at most? . There are faster algorithms such as a modiication to Manacher’s algorithm but if you use the algorithm, you will have to state the entire algorithm, and prove its correctness and running time. |
2.2 [12 marks] A palindromic decomposition of a string w is a partition of w into substrings u1 , . . . , um such that w = u1 . . . um and each part ui forms a palindrome. For example, if w = abcbabaab, then u1 = a, u2 = bcb, u3 = a, u4 = baab is a palindromic decomposition of w.
We assign each substring ui a cost denoted by cost(|ui |), where |ui | is the length of ui . Finally, we deine the cost of a decomposition u1 , . . . , um to be the sum of the costs of the individual substrings ui ; that is, if w = u1 . . . um , then the cost of the decomposition is
cost(|u1 |) + ··· + cost(|um |).
We want to ind the minimum cost of a palindromic decomposition of w. Given a string w = w1 . . . wn and an array of all costs, design an O(n2 ) algorithm to compute the minimum cost of a palindromic decomposition of w.
|
Hint. Perform a pre-processing step using 2.1. |
Question 3
You are participating in a robotics competition, and need to program a robot to move through an m by n grid. The robot starts at cell (1, 1), and must reach cell (m, n) to inish.
Your robot accepts two types of instructions:
. Start moving down at cell (i, j),
. Start moving right at cell (i, j).
An instruction is not required to tell the robot which way to move at the start, as there is only one possibility based on the irst turning instruction.
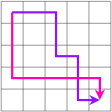
For example, in this grid with m = n = 5, the purple path requires four instructions (down at (1, 3), right at (3, 3), down at (3, 4), right at (4, 4)) while the pink path requires two (right at (4, 1), down at (4, 5)).
3.1 [6 marks] Design an algorithm that runs in O(mn) time and determines the number of distinct paths through the grid that the robot can traverse.
|
Hint. A closed form solution is possible, but we naturally encourage the use of Dynamic Programming which will assist with the rest of the question. A similar problem will also be discussed in the Week 8 Tutorial. Consider the 4 ways to reach a cell (i, j). |
3.2 [8 marks] Unfortunately due to rising inlation your robot now only has a limited amount of memory, and can only store r instructions. Design an algorithm that runs in O(mnr) time and determines the number of distinct paths through the grid that the robot can traverse using at most r instructions.
3.3 [6 marks] To make the competition more interesting, Blake has placed obstacles in some of the cells, which the robot is unable to pass through. They have given you an array O[1 . . . m][1 . . . n], where O[i][j] is True if cell (i, j) has an obstacle and False otherwise. Of course, Blake has made sure that a robot can travel from (1, 1) to (m, n) by moving only right and down.
You wish to ind the smallest amount of memory r that your robot needs to be able to traverse the grid.
Design an algorithm that runsin O(mnr) time and inds the smallest number of instructions needed to traverse the grid.
|
Note that the parameter r in the time complexity is also the answer your algorithm is trying to ind. This is similar to the Ford-Fulkerson algorithm for max low, where the time complexity is dependent on the max low for the given graph. An algorithm that runs in O(mn(m + n)) will be eligible for at most 4 marks for this part. |
2023-07-27