Math 142 Exam 2 Summer 2017
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
1. A population N(t) satisfies ![]() = Nf(N) where f is graphed below.
= Nf(N) where f is graphed below.
(a) (7 points) Find all equilibria for N.
(b) (5 points) Which equilibria are stable?
2. Let  be a 3-dimensional vector whose components are the population of frogs, aged 0, 1, and 2 years. The population is modeled by
be a 3-dimensional vector whose components are the population of frogs, aged 0, 1, and 2 years. The population is modeled by  +1 = A
+1 = A . Suppose that A has eigenvalues λ1 = −2, λ2 = 2, λ3 = 3 with eigenvectors
. Suppose that A has eigenvalues λ1 = −2, λ2 = 2, λ3 = 3 with eigenvectors
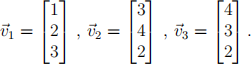
(a) (5 points) Write down a general expression for xk .
(b) (10 points) Use your expression to find the ratio of frogs of age 2 years to the number of frogs in the total population.
3. Consider the nonlinear difference equation
Nk+1 = Nk (3 − Nk − 1 ).
(a) (5 points) Solve for the positive equilibrium L > 0.
(b) (7 points) Find the linearized equation around L by setting Nk = L + εxk .
(c) (7 points) Find the general solution for xk . Is the equilibrium stable?
4. Consider the Predator-Prey system.

(a) (10 points) Write F = 2 + εx(t) and S = 1 + εy(t) and derive linearized equations for x and y.
(b) (10 points) Solve for x(t), and show that the equilibrium is stable.
5. (10 points) The following Predator-Prey system has periodic solutions for F (t) and S(t).
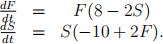
Show that the average value of F (t) over its period is equal to its equilibrium value.
6. (10 points) We model populations K(t), F (t), and W (t) of Krill, Fish, and Whales.
• Krill compete with fish for resources and have unlimited growth if no fish or whales are present.
• Fish compete with whales for resources and have logistic growth if no krill or fish are present.
• Whales eat krill but do not eat fish.
Write a system of equations that models these populations.
7. A competing species equation

(a) (12 points) Use Nullclines to sketch the general solution in the phase plane.
(b) (3 points) Sketch y(t) if x(0) = 1 and y(0) = 2.
2023-07-25